Merhaba sevgili e-bergi okurları! Sizlere bu ay bilgisayar biliminde çok önemli bir yere sahip olan, hem veri yapısı hem de bir sıralama algoritması olarak bilinen yığından (heap) bahsedeceğim. Kendi içinde birkaç türü olsa da bu yazımda konunun temel mantığını en anlaşılır şekilde aktarabileceğim ve yığının en yaygın türü olan ikili yığını (binary heap) anlatacağım.
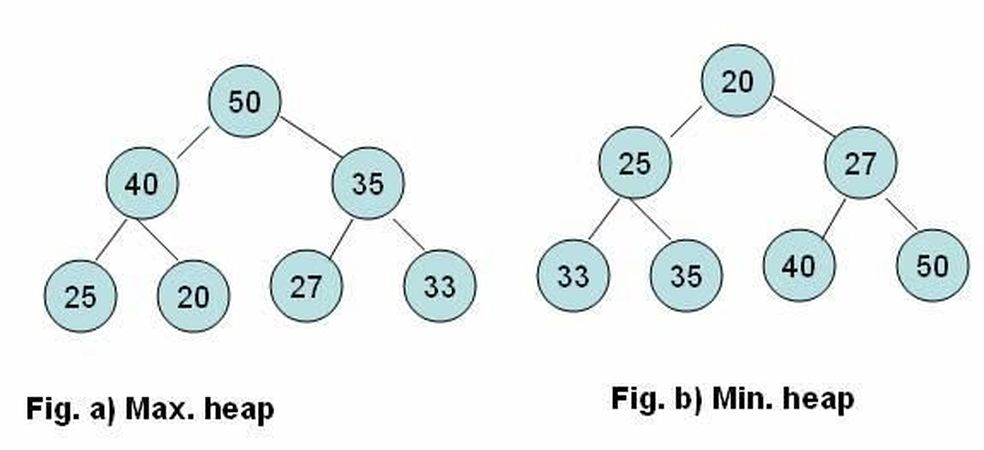
Yığın, temelde ağaç veri yapısıyla oluşturulur; ancak bu ağaçlar kendi özelliklerinin yanı sıra yine heap adı verilen bir başka özelliğe sahiptir. Heap özelliği, sıralamamızı azalan veya artan şeklinde yapmamıza göre max-heap veya min-heap olarak ifade edilir. İkisi de çok benzer şekilde çalıştıkları için sadece birini anlatmam yeterli olacaktır; bu yüzden yazımın geri kalanını min-heap üzerinden anlatacağım. Min-heap özelliği, ağacın herhangi iki düğümünü aldığınızda (X ve Y diyelim isimlerine) eğer X, Y'nin çocuğuysa X düğümünün değerinin Y düğümünün değerinden daha büyük veya ona eşit olmasıdır. Bu şekilde olduğunda herhangi bir düğümden ağacın köküne doğru ilerlersek değerin asla artmaması gerekir. Bu da bize kökün minimum değere sahip olduğunu söyler. Min-heap’i anlattığıma göre ikili heap’e geçelim. İkili heap, aslında tahmin edeceğiniz üzere min-heap yapısının ikili ağaçlar (binary tree) üzerinde uygulanmış olanına denir. İkili ağaçlarda herhangi bir düğüm en fazla iki tane çocuğa sahip olabilir. İkili heap az sonra anlatacağım heap operasyonlarının doğası gereği tam ikili ağaçlardır (complete binary tree). Hatırlatmak için kısa bir not daha: en alt iki seviyedeki düğümler hariç tüm düğümlerinin tam olarak iki çocuğu olan ve en alt seviyesindeki düğümleri ağaca soldan sağa eklenen ikili ağaçlara tam ikili ağaçlar denir.
Yığında yapılan işlemlere geçmeden önce cevaplamamız gereken iki tane önemli soru var: neden ve ne zaman kullanılmasının gerektiği. Sıralama algoritması olarak yığının önemli bir özelliği yersel karmaşıklığının sabit olmasıdır; yani girdinin büyüklüğü ne olursa olsun yığının ihtiyaç duyduğu ek hafıza alanı sabittir. Yığının zamansal karmaşıklığını düşünecek olursak en iyi durumda da n*log(n)'dir, en kötü durumda da. Dolayısıyla bilinen en iyi sıralama algoritmalarından biridir; ancak min-heap'in tercih edilmesinin sebebi sıralama algoritması olmasından ziyade her zaman en küçük elemanı kökte tutmasıdır. Yani yığının uygulanacağı yerin genelde buna benzer bir ihtiyacı vardır. Fırsatçı (greedy) yaklaşımla oluşturulmuş algoritmalar her zaman yereldeki en uygun değer üzerinden ilerler. Dolayısıyla en uygun değer bir şekilde minimum veya maksimum değer olarak tanımlanabiliyorsa min-heap veya max-heap buralarda önemli işler görür. Biraz daha genellersek; eğer elimizde bir liste dolusu elemanımız varsa ve bunları da belli bir önceliğe göre sıralı olarak işlememiz gerekiyorsa heap'i kullanabiliriz. Zaten heap sıralamasının bir diğer adı da öncelik kuyruğudur (priority queue) . Burada yığının diğer sıralama algoritmalarından farklı olarak dikkat etmemiz gereken noktası şudur; önceliklere göre yapılacak olan sıralamayı hemen yapmak zorunda değiliz. İşledikçe zamanla sıralasak da olur. Şimdi yığın bu gibi yetenekleri hangi işlemlerle nasıl elde ediyor onu görelim.
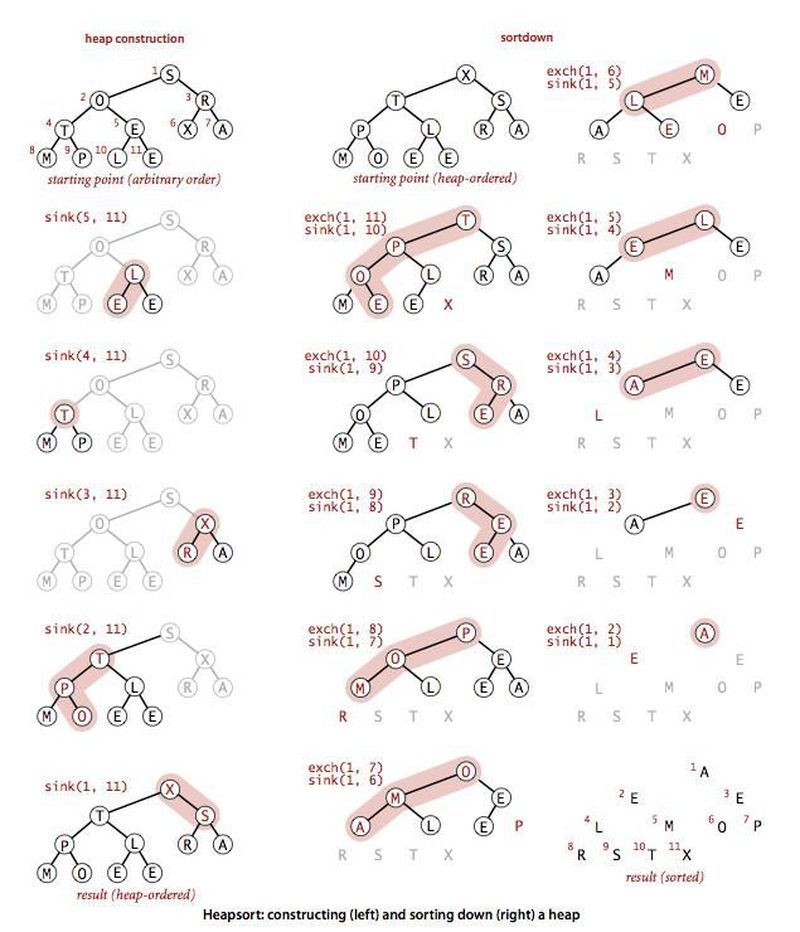
Bir min-heap yapısında genellikle uygulanan işlemler şunlardır: en küçük elemana (yani köke) ulaşma, en küçük elemanı ağaçtan çıkartma, bir düğümün değerini güncelleme ve ağaca yeni bir düğüm ekleme. Bu işlemlerin nasıl yapıldığını açıklamadan önce tam ikili ağaçlar üzerinde çalışıyor olmamızın bir getirisinden bahsetmem gerekiyor; böylece birazdan işlemleri açıkladığımda kafa karışıklığı olmaz. Tam ikili ağaçlar bir dizi ile ifade edilebilir; yani kullanılan veri yapısı ağaç olarak oluşturulmak zorunda değildir. Yığın yapısında yapacağımız her bir işlemi esnek bir dizi üzerinde de yapabiliriz. Bu sayede ağaçtaki her bir düğümün bir anahtar değeri (index) de olmuş olur. Daha da ilginci, yığın yapısını esnek bir dizi uygulayarak oluşturduğumuzda bu anahtar değerlerini kullanarak düğümlerin çocuklarını ve ebeveynini bulabiliyor olmamız. Anahtar değerlerinin 1'den başladığını ve n tane düğümümüzün olduğunu varsayalım. O zaman 1. sıraya kök düğümü yerleştiririz ve onun çocuklarını 2 ve 3'e yerleştiririz. Daha sonra ikincinin çocuklarını 4. ve 5. sıralara, 3. düğümün çocuklarını da 6. ve 7. Sıraya yerleştirir, böylece “sığ öncelikli” olarak da bilinen şekilde; yani derinliği en düşük olanlara öncelik vererek bütün diziyi doldururuz. Bu şekilde yaptığımızda dikkat edersek herhangi bir düğümün anahtar değeri i ise çocuklarının anahtar değerleri 2*i ve 2*i+1 olmaktadır. Benzer şekilde i. düğümün ebeveyn düğümü de eğer i çiftse i/2, i tekse (i-1)/2 anahtar değeri olan düğüm olmaktadır. Yığını bir ağaç değil de dizi olarak düşündüğümüzde artık “son düğüm” gibi laflar etmemde bir sakınca kalmamaktadır; çünkü son düğüm anahtar değeri en büyük olan düğümdür. Bu yöntemle bütün tam ikili ağaçları dizilere çevirebileceğimizden bu iki yapının işlemleri arasında önemli bir fark yoktur. Ben de yığında yapılabilecek işlemleri, veri yapısı olarak da daha kolay olduğundan diziler üzerinde anlatacağım. Nihayet işlemlere geçebiliriz! :)
En Küçük Elemanı Bulma
Yukarıda anlattığım üzere aslında en küçük elemana ulaşmak köke ulaşmaktır ve kök her zaman dizinin ilk anahtar değerine sahip diliminde bulunur. Dolayısıyla köke ulaşma operasyonu sabit zaman alan bir işlemdir.
En Küçük Elemanı Silme
En küçük elemanı diziden çıkartmak için dizinin son elemanını alırsınız ve ilkinin üzerine yazarsınız. Sonra dizinin boyutunu en son elemanı yok edecek şekilde bir azaltırsınız. Ancak bahsettiğim taşımayı yapmak çok büyük ihtimalle min-heap özelliğini bozacağından yığın yapısı bu özelliğini koruyor mu diye kontrol etmeniz gerekmektedir. Bunun için de sadece ilk elemanın iki çocuğundan küçük olup olmadığını kontrol etmeniz yeterli. En az bir çocuğundan büyükse çocuklarından küçük olanıyla yer değiştirirsiniz. Sonra tekrar çocuklarının değerinden küçük mü diye kontrol etmeniz gerekir ve yine en az bir çocuğundan büyükse çocuklarından küçüğüyle yerlerini değiştirirsiniz. Sonunda ya tüm çocuklarından büyük olduğunda ya da artık çocuğu kalmadığında bu döngüyü bitirirsiniz. Tam ikili ağaçların derinliği log(n) olduğu için en fazla log(n) adımda bu koşullardan biri gerçekleşeceğinden bu işlemin zamansal karmaşıklığı log(n) kadardır.
Eleman Değeri Güncelleme
Bir elemanın değerini güncellediğimizde yine ilk olarak bu yaptığımız değişiklik yığın (heap) özelliğini bozmuş mu -yani ebeveyninden büyük ve çocuklarından küçük mü- diye kontrol ederiz. Özellik bozulmadıysa zaten bir şey yapmaya gerek yoktur; ancak eğer güncellenen düğüm ebeveyninden küçükse ebeveyniyle yerleri değiştirilir ve yeni ebeveyniyle kıyaslanır. Ebeveyninden küçük olduğu sürece veya köke ulaşmadığımız sürece yeni kök yer değiştirilerek yukarı doğru taşınır ve sonunda yığın yapısının özelliği tekrar sağlanmış olur. Aksine eğer güncellenen düğüm çocuklarının en az birinden büyükse, bunlardan küçük olan çocuğuyla yerleri değiştirilir ve tekrar çocuklarıyla kıyaslanır. Tüm çocuklarından küçük olana kadar ya da yapraklara ulaşana kadar aşağıya doğru yeri değiştirilir. Sonunda özellik tekrar sağlanmış olur. Bu işlem de en fazla log(n) adımda yapılır ve karmaşıklığı log(n)'dir.
Eleman Ekleme
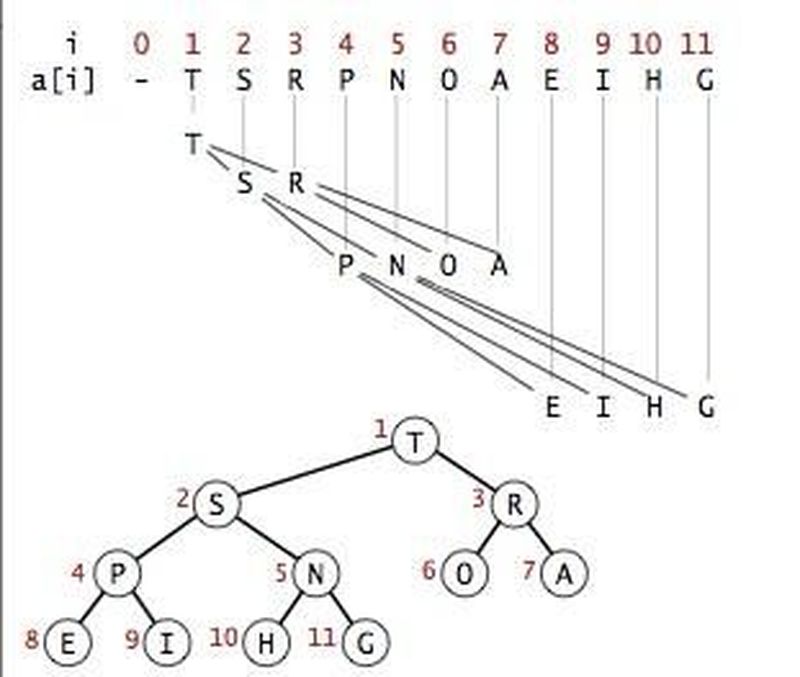
Diziye yeni bir eleman eklerken bu elemanı önce en sona ekleriz. Daha sonra ebeveyninden küçük mü diye kontrol ederiz. Eğer ebeveyninden küçükse onunla ebeveyniyle yerlerini değiştiririz ve tekrar yeni ebeveyninden küçük mü diye kontrol ederiz. Bu şekilde köke yani anahtar değeri en küçük olan düğüme ulaşana kadar ya da ebeveyninin değeri kendi değerinden küçük olana kadar devam ederiz. Burada da ağacın derinliği log(n) olduğu için bu işlem de en fazla log(n) adım sürecektir. Dolayısıyla bu operasyonun da zamansal karmaşıklığı log(n)'dir.
Fark ettiğiniz üzere bir sıralama algoritması olması rağmen “şu şekilde sıralamış olur” gibi bir laf etmedim; çünkü yukarıda da bahsettiğim üzere yığın aslında bireylere sıralı bir şekilde ulaşırken daha çok gereklidir. İşlemleri kendi uygulamanıza özel bir şekilde, gerektikçe kullanırsınız. Yine de, illa sıralamak istiyorum diyorsanız (bir anlamda uygulamanız buysa:) ) şu şekilde yapmak mümkün: elinizdeki sıralanacak listeyi dizi şeklinde bir yığın yapısı haline getirip en küçük elemanını –en küçük anahtar değerli olanını- sürekli olarak bir başka dizinin arkasına ekler ve ardından o en küçük elemanı yığın yapısından çıkarırsanız yığınınız boşaldığında elinizdeki ikinci dizi küçükten büyüğe sıralı hale gelmiş olur. (bu yöntemin özünde yatan ilke her seferinde kalan elemanların en küçüğünü alıyor olmamızdır)
Bu ayki yazımın sonuna geldik. Bir sonraki sayımızda tekrar görüşmek üzere; kendinize iyi bakın.