Merhaba değerli e-bergi okurları! Geçen sayımızda yapay zeka alanının önemli keşifsel yaklaşımlarından A* yönteminden bahsetmiştik. Bu sayımızda da yapay zeka ve robotik dallarının popüler problemlerinden Takipçi-Kaçak Problemi'ni (Pursuer-Evader Problem) öğreneceğiz. Bu problemde amaç, belirli bir alan içinde yeri belirli olmayan hareketli bir veya birden fazla aktörün yerlerini, bir veya birden fazla takipçi aktörle belirlemektir ¹. Gerçek dünyada da özellikle savunma sanayisinde alan tarama ve yer belirleme gibi amaçlarla sıkça kullanılmaktadır.

Problemin çözümüne geçmeden önce problemi daha detaylı olarak tanımlamak yararlı olacaktır. Bu problemde amacımız, bir veya birden fazla takipçiye, tamamen tahmin edilemez bir şekilde ilerleyen kaçağın yerini en iyi bir şekilde belirleyebilmesi için bir rota planı sağlamaktır. Bu yazıda problemi genel açıdan tanımlayıp onunla ilgili varsayımlardan ve kurallardan bahsedip, tek takipçi ve tek kaçak olan bir örnek için bu problemin çözümünün nasıl yapılabileceğinden bahsedeceğiz. Bu problemde kullanacağımız varsayımlar ve kurallar aşağıdaki gibi olacaklar:

• Problemi tek bir takipçi ve tek bir kaçak olan bir alanda çözeceğiz.
• İçinde bulancağımız alan çokgensel bir şekile sahip olacak ve basit bir şekil olacak. Burda basitten kasıt, çokgensel şeklin içinde ondan kopuk ayrıca şekiller bulunamayacaktır. Alan tek bir parçadan oluşan bir çokgensel şekilden oluşacaktır.
• Kaçaklar herhangi bir hızda hareket edebilirler, ancak bir yerden bir yere ışınlanamazlar; yani hareketleri sürekli olmak zorunda olacaktır.
• Takipçilerin sensör limitleri sınırsız olacaktır; yani önlerine bir engel çıkmadıkça alanın sonuna kadar görüş mesafeleri olacaktır.

Problemi daha iyi anlayabilmek ve izleyeceğimiz yöntemi gözümüzde canlandırabilmek için yukarda bahsedilen varsayımları bir de şekil üzerinde görelim.

Şekil-1'de gri ile sınırlandırılmış basit bir çokgensel dünyayı görmek mümkün. Şekilden de fark edilebildiği gibi dünyamız, içerisinde kopukluklar içermiyor. Sol alt köşeden yukarıya, iki engelin ortasına doğru ilerleyen nesne ile gösterilen şey takipçi. Yukarıda da bahsedildiği gibi, takipçi önüne engel çıkmadıkça sonsuz görüş mesafesine sahip; bu sebeple açık yeşil ile gösterilen alanlar takipçinin o anki görüş alanını simgeliyor. Engel sebebiyle göremediği alanlar şekilde koyu yeşlle çizilmiş. Unutmadan belirteyim, bu problemde iki önemli terim var: temizlenmiş alan ve temizlenmemiş alan. Bu terimlerden temizlenmiş alan daha önceden ziyaret ettiğimiz ve kaçak vasıtanın halen orada olmadığına emin olduğumuz alanlara verilen bir isim. Ancak karıştırılmaması gereken bir nokta: temizlenmiş alan daha önceden ziyaret ettiğimiz her yer değil, halen kaçak vasıtanın orada olmadığından emin olduğumuz alandır. Örnek vermek gerekirse Şekil-1’deki dünyada takipçi beyaz ile gösterilen alandan şu anki pozisyonuna geçerken, kaçak vasıta takipçiye görünmeden hiçbir şekilde o alana geçemez; çünkü ışınlanma özelliğine sahip değil. Bu sebeple de o temizlenmiş alan beyaz ile çizilmiş.

Problemimizi formülize ederken dünyayı 3 farklı alanın birleşimi şeklinde göstereceğiz: temizlenmiş alanlar, şu an görüş alanımızda olan alanlar ve temizlenmemiş (kaçak vasıtanın içerisinde bulunabilme olasılığı olan) alanlar.

Bu problemi çözebilmemiz için elimize verilen alanı ortak özellikleri olan parçalara belirli bir şekilde ayrımamız gerekmekte. Yani, belirli şeylerin gelişmediği alanlarda -o alanın neresinde olduğumuzun önemi olmayacağından- elimizdeki dünyayı bu şekilde alanlara ayırıp daha sonra bu alanlardan oluşan çizge üzerinde işlem yapmak mantıklı olacaktır. Alanı bu şekilde parçalara bölebilmek için geçit köşelerinden(gap edges) yararlanacağız. Geçit köşeleri o anda bulunduğumuz görüş alanımızın köşeleridir ve 0 veya 1 değeri alabilirler. Eğer görüş alanımızla birleştirdiği alan temizlemiş bir alan ise geçit köşesinin değeri 0, eğer görüş alanımıza birleştirdiği alan temizlenmemiş bir alan ise geçit köşesinin değeri 1 olacaktır. Şekil-1’e bakarsak sol üst taraftaki geçit köşesinin değeri 0, alttaki iki geçit köşesinin değeri 1’dir. Şekilde bu değerler gösterilmediğinden Şekil-2'de geçit köşelerini daha rahat bir şekilde inceleyebilirsiniz.

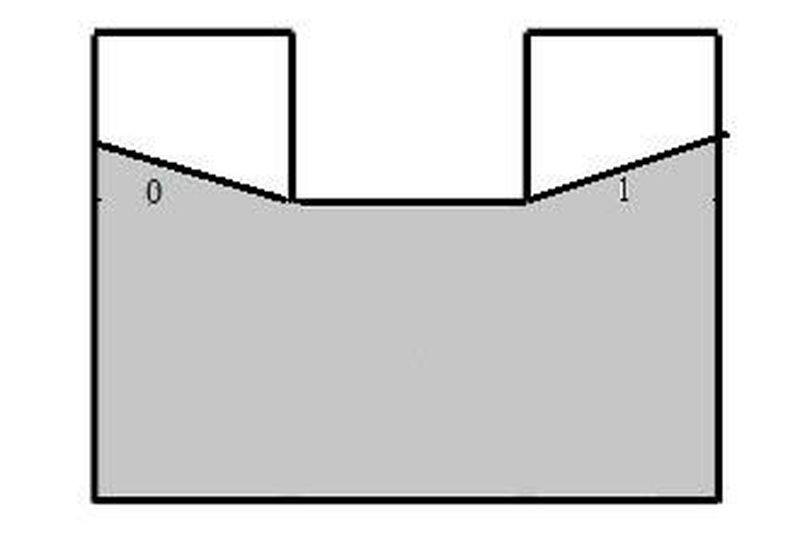
Şekil-2'deki senaryoda takipçi gri ile gösterilen alanda bir yerde durmaktadır. Soldaki geçit köşesi 0 olduğundan o bölgeye takipçinin daha önceden uğrayıp oranın temiz olduğunu anladığını ve 1 ile gösterilen geçit köşesiyle geçebileceğimiz alana ise henüz uğramadığını anlıyoruz. Aslında bu durumda, eğer dünyamızda bir kaçak vasıta var ise onun 1 ile gösterilen geçit köşesinin olduğu köşede olduğunu anlayabiliriz. Elimizdeki dünyayı tamamen bir bilgi çizgesine çevirebilirsek eğer, bu çizge üzerinde -tıpkı demin bulduğumuz gibi- kaçak vasıtanın olabileceği yeri hedef düğümü olarak seçerek oraya ilerlemek bize çözümü verecektir.

Şekil-2'deki dünyayı eğer parçalamak istersek bunu, içinde bulunduğumuz sürece bize ek bilgi getirmeyen bölgeleri birer düğüm gibi alarak dünyayı düğümlere bölmemiz gerekir. Bunu dünyamıza uyguladığımızda Şekil-3’teki gibi 5 parçaya bölebileceğimizi anlarız.

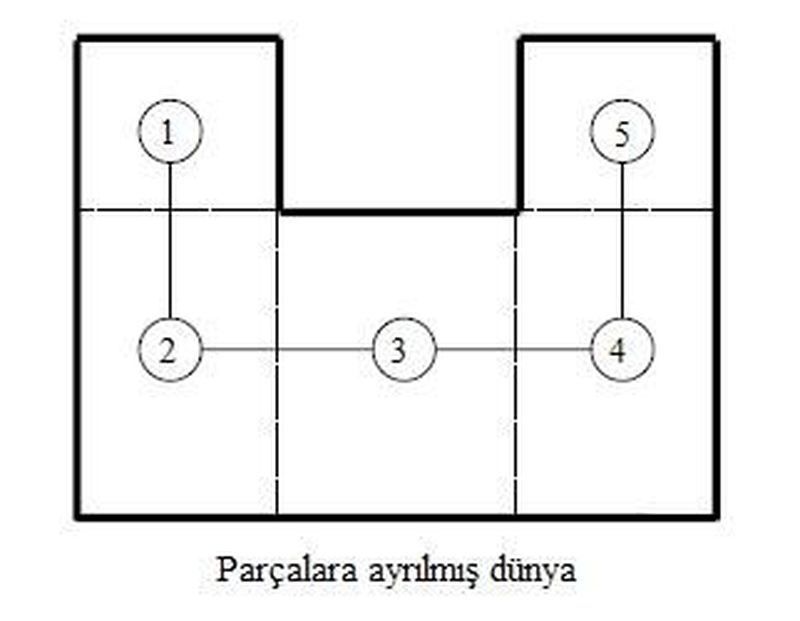
Dünyamızı parçalara ayırırken bu şekilde 5 bölge oluşur; çünkü ancak bu bölgelerden diğerine geçerken bilgi değişimi olmaktadır. Mesela 1 numaralı bölgeden 2 numaralı bölgeye geçerken bir bilgi değişimi olur; çünkü daha önce sadece 2 numaralı bölgeyi görebilirken -2 numaralı bölgeye geçince- artık 3 ve 4 numaralı bölgeleri de görebilmeye başlarız. Diğer bölgelerde de bu gibi durumlar olduğundan alanı 5 bölgeye ayırırız. Bu 5 bölge geçit köşelerindeki değerlere göre çizgede değer alacaklardır. Çizgemizi oluştururken geldiğimiz bölge değil, oradan gidebileceğimiz bölgenin değerlerine göre çizge değerleri atanacaktır. Genelde 3 numaralı bölgeden başlayacağımızdan ve 3 numaralı çizgeden başladığımızda oraya hiçbir yerden gelmiş olmayacağımızdan o bölgenin durumunu 2 geçit köşesi değeriyle belirteceğiz: 2 ve 4 numaralı bölgelere geçişte kullanılan geçit köşeleri. Diğer köşelerde ise bir bölgeden gelinip diğerine geçileceğinden durumu tek geçit köşeşi değeriyle göstermek mümkündür. 3 numaralı bölge için olası durumlar 11, 01, 10 ve 00’dır. Soldaki değerin 2 numaralı bölge için verilen değer olduğunu düşünürsek, 11 hem 2. hem de 4. bölgenin henüz temizlenmediğini göstermektedir. Aslında her zaman başlangıçta olacağımız durum değeri bu olacaktır; çünkü başlangıçta henüz hiçbir yeri ziyaret etmemiş durumdayız. 2 bölgesini ziyaret edip o bölgenin temiz olduğuna karar vermiş bir şekilde 3. bölgeye dönersek bu sefer 3. bölgedeki durumumuz (bilgimiz) 01 olacaktır. Amacımız 3. bölgede 00’a ulaşmak, yani her iki tarafın da temiz olduğunu garantilemek. Eğer bir kaçak varsa zaten bir tarafı temizledikten sonra onu göreceğimizden yerini tespit edebiliriz ve bu nedenle alanın temiz olduğunu bu şekilde göstermek daha kullanışlı olacaktır. Diğer bölgelerde, yani 1, 2, 4 ve 5’te tek durum değeri (0 ya da 1) yeterli olacaktır. Bütün bu anlattıklarımızla oluşacak olan çizge Şekil-4’te görülebilmektedir.

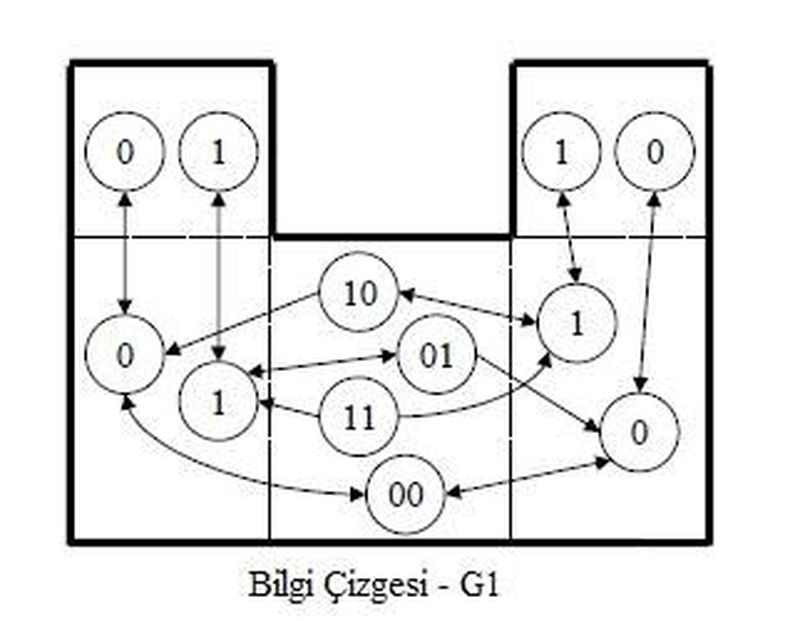
Her ne kadar karmaşık görünse de aslında Şekil-4’de görülen çizge yukarıda anlattıklarımın özetidir. Demin de bahsettiğim gibi 3. bölgeden 11 durumuyla başlarız. Eğer 2. bölgeye geçeceksek -henüz ikinci bölgenin üstünü göremediğimizden- oradaki geçit köşesinin değeri 1 olacak, bu sebeple de 2. bölgenin durumu 1 olacaktır. Yani çizge üzerinde bu sebeple 11’den 2. bölgedeki 1’e doğru bir bağlantı vardır. Aynı şekilde 2. bölgede 1 durumundayken ve 1. bölgeye çıkarken gene durumumuz 1 olur; çünkü 1. bölgenin komşu olduğu 2. bölgenin geçit çizgisi -4. bölgenin değeri bilinmediğinden- hala 1’dir. Daha sonra aynı şekilde 2. bölgeye geçilir; ancak bu kez 2. bölgeden 3. bölgeye geçilirken artık o tarafta kaçağın olmadığına emin olduğumuzdan durumumuz 01’e gelir. 2. bölgedeki geçişlerimizin aynılarını yaparak 4. ve 5. bölgelere de ilerleyebiliriz. Şekil-4’te tüm olası başlangıçlara ve gidişlere göre bu bağlantılar sağlanmıştır. Bu dünyada herhangi bir durumda başlandığında artık hedef sadece 00'a, veya diğer dünyalar için 0’a ulaşmaktır. İçinde 1 içermeyen bir duruma ulaşıldığında dünyanın tamamının temizlendiği garanti edilmiş olur.

Tabii bu anlattığımız çözüm sadece basit bir dünya içindi. Daha karmaşık ve girinti sayısı fazla olan dünyalar için tek bir takipçi ile bu tip bir çizge çıkarmak mümkün olmayabilir. Onlar için de aynı mantıkla daha karmaşık çözümler bulmak mümkündür; hatta bu tip çalışmalar için çözümler halen önerilmekte ve çalışmalar yapılmaktadır.

Eğer bu problem ilginizi çekmişse ve daha karmaşık biçimleriyle ilgili bilgi edinmek isterseniz aşağıdaki 3 numaralı kaynak sizin için iyi bir başlangıç noktası olacaktır.

Bir sonraki yazımızda görüşmek üzere, kendinize iyi bakın!

Referanslar

1. http://en.wikipedia.org/wiki/Pursuit-evasion
2. http://www.cs.cmu.edu/~motionplanning/lecture/Chap6-CellDecomp_howie.pdf
3. "A Visibility-Based Pursuit-Evasion Problem" Guibas, Latombe, LaValle, Lin, Motwani