Merhaba sevgili e-bergi okuyucuları! Bu ayki yazımda sonlu özdevinir(finite automata) kavramını açıklayıp, 2 ana alt grubu olan kararlı sonlu özdevinirler ve kararsız sonlu özdevinirler hakkında genel bilgi vereceğim.

En basit tanımıyla, bir sonlu özdevinir girdi olarak karakter dizisi(string) alıp belli kurallarla belli durumlar arasında ilerleyip esasen çıktı vermeyen; ancak karakter dizisinin dile göre geçerli olmadığını anlamamızı sağlayan bir tür makinedir. Bir sonlu özdevinirin en önemli özelliği ise hafızaya ihtiyaç duymamasıdır.

Daha iyi anlayabilmek için bir sonlu özdevinirin çalışma mantığını açıklayalım;

Elimizde abaab şeklinde bir dizi karakter ve q0 q1 ...qn isimli durumlarımız olsun. En başta kontrol mekanizmamızda başlangıç durumu hangi q ise o q’dan başlanır. Bir okuma imleci ile önce ilk karakterden (a) başlamak üzere teker teker karakterler alınır, elemana ve bulunan duruma göre yeni duruma geçilir ve girdiler bitene kadar işlemler bu şekilde devam eder. Girdiler bittiğinde ise makine eğer bitiş için geçerli olarak tanımlanmış bir durumda kalmışsa bu karakter dizisi kurallarına göre kontrol ettiğimiz dile uygundur.

Biraz daha ayrıntılarıyla ve örnekleriyle inceleyelim. Sonlu özdevinirler 2 grupta incelenirler:

  1. Kararlı sonlu özdevinirler(Deterministic Finite Automata)
  2. Kararsız sonlu özdevinirler(Nondeterministic Finite Automata)

Kararlı Sonlu Özdevinirler

Bir kararlı sonlu özdevinir makinesi M=(K,∑,δ,s,F) şeklinde tanımladığımız beşli bir yapıdır. Tanımdaki ifadeler ise şu anlamlara gelir;

K: Durumların sınırlı kümesi

∑:Alfabe

δ:Geçiş fonksiyonu, K kümesindeki bir durumdan ∑ kümesindeki bir elemana göre yine K kümesinden bir duruma geçiş fonksiyonudur.

s:K'nın bir elemanı olan başlangıç durumu

F: K'nın bir alt kümesi olan bitiş durumlarının kümesi

Makinenin o anki halini konfigürasyon gösterir. Başka bir deyişle konfigürasyon makinenin hangi durumda bulunduğunu ve geriye kalan karakter dizisini gösterir. Örnek: ( q2,abaa)

2 konfigürasyon arasındaki ilişkiyi ise ikili ilişki(binary relation) gösterir. Yani eğer (q,w) konfigürasyonundan (p,v) konfigürasyonuna geçiş varsa ikili ilişki (q,w)⊢M(p,v) şekline gösterilir ki bu durumda w=av ise δ(q,a)=p olur.

Şimdi ise bir örnek ile bir karakter dizisinin bir makine için geçerli olup olmadığına bakalım.

K={q0 ,q1}  ∑={a,b}  s= q0  F= {q0}   olsun.

Fonksiyonlarımız ise  δ(q0,a)= q0    δ(q0,b)=q1  δ(q1,a)= q1  δ(q1,b)= q0

Bu durumda “abab” şeklinde bir karakter dizisi tanımladığımız kararlı sonlu özdevinire uygun mudur?

( q0 ,abab)⊢M( q0 ,bab)⊢M( q1,ab)⊢M( q1,b)⊢M( q0 ,e)

q0 F kümesinin elemanı olduğu için “abab” karakter dizisi de bu dile uygundur.

Kararsız Sonlu Özdevinirler

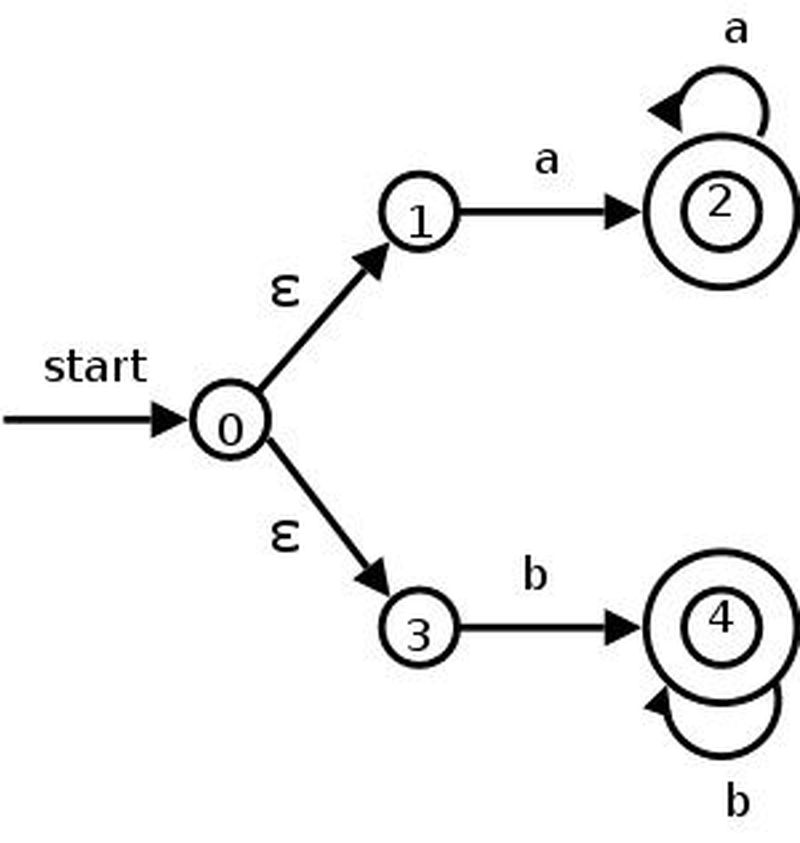
Bir kararsız sonlu özdevinir makinesi M=(K,∑,∆,s,F) şeklinde tanımladığımız beşli bir yapıdır:

K: Durumların sınırlı kümesi

∑:Alfabe

∆:Geçiş fonksiyonu, K kümesindeki bir durumdan ∑ kümesindeki bir elemana göre veya boş elemanla (e) yine K kümesinden bir duruma geçiş fonksiyonudur.

s:K'nın bir elemanı olan başlangıç durumu

F: K'nın bir alt kümesi olan bitiş durumlarının kümesi

Kararsız sonlu özdevinirler için konfigürasyn K x ∑* kümesinin bir elemanıdır. 2 konfigürasyon arasındaki ilişki de (q,w)⊢M(p,v) şekline gösterilir ki bu durumda w=av ve a∈ (∑∪{e}) ise (q,a,p)∈∆ olur.

Özetle kararlı sonlu özdevinirler ve kararsız sonlu özdevinirler arasındaki farklar şöyledir. Birincisi, kararlı sonlu özdevinirlerde her durum için olası tüm alfabe elemanlarına ulaşılabilecek bir durum tanımlanmıştır. İkincisi ise kararsız sonlu özdevinirlerde boş eleman(e) ile durum değişebilmesidir. Ayrıca, bir kararsız sonlu devinirde bir harf ile birden fazla duruma gitmek söz konusudur.

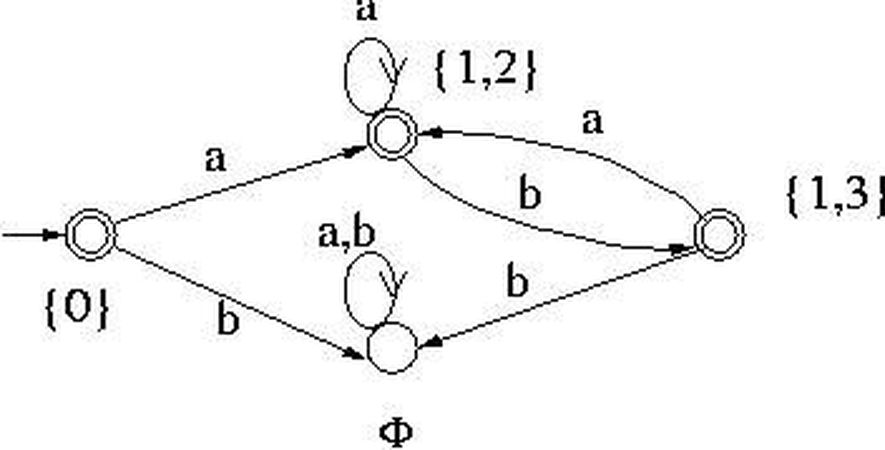
Şunu da bilmek gerekir ki her kararsız sonlu ödevinir için bir kararlı sonlu özdevinir kurulabilir. Bu sırada, özetle, e ile ulaşılabilen durumları tek durumda toplamak ve eksik fonksiyonlar için bitiş durumuna gitmeyen yeni durum ve fonksiyonlar eklemek gerekir. Sonrasında elde edilen kararlı sonlu özdevinir basitleştirilip daha verimli bir kararlı sonlu özdevinir de elde edilebilir. Bir dahaki ayda bunlar hakkında daha ayrıntılı bilgi vereceğim.

Kaynaklar