Merhaba e-bergi okurları! Bu yazımda sizlere matematiksel denklemlerin köklerini -çok küçük bir hata payıyla da olsa- bulmak için harika bir yoldan bahsedeceğim. Her yerde karşımıza çıkan Isaac Newton amcamız, bu işe de el atmış ve bizleri büyük zahmetlerden kurtarmış.
Tanımı
Yöntemin temelini tahmin yürütülerek elde edilen bir kökten yola çıkarak gerçek bir köke olabildiğince yaklaşmak oluşturmakta.
f, [a,b] aralığında, gerçel sayılar kümesine tanımlı ve türevlenebilir bir fonksiyon, x_0 ise bizim ilk tahminimiz olsun.
x_1 = x_0 - (f(x_0) / f'(x_0))Buradaki x_1, asıl köke tahminimiz olan x_0'dan daha yakın olan kök değeridir. Aynı işlemi bir daha yapalım:
x_2 = x_1 - (f(x_1) / f'(x_1))Ne kadar çok yaparsak, asıl köke o kadar yakın bir sonuç buluruz. Genel bir tanım yapmamız gerekirse:
x_(n+1) = x_n - (f(x_n) / f'(x_n))Çıkış Noktası
Formülün nereden geldiğine bakacak olursak:
Fonksiyonumuz f, asıl kökümüz r ve tahminimiz x_0 idi.Fonksiyona (x_0,f(x_0)) noktasında bir teğet çizersek bu teğetin x eksenini kestiği nokta olan x_1, görünüş itibariyle r'ye x_0'dan daha yakın.
Türevin grafiksel anlamı olan bu teğetin eğimini yazacak olursak:
f'(x_0)=f(x_0) / (x_0 - x_1)Buradan x_1'i çekecek olursak:
x_1 = x_0 - (f(x_0) / f'(x_0))Bu formülü genelleştirdiğimizde yukarıdaki tanım kısmında verilen formülü elde ediyoruz.
Kullanımı
Bu yöntem, birçok denklem çözümünde bize bir hayli yardımcı oluyor.Sadece birkaç adımda asıl köke çok yakın değerler elde edebiliyoruz. Ayrıca bu yöntem yalnızca denklemin kendi köklerini bulmaya değil, yerel minimum ve maksimum noktalarını belirlemeye de yarıyor.Bulmak istediğimiz noktalar bir bakımdan f fonksiyonunun değil de f fonksiyonunun türevinin kökleri olduğundan, tek yapmamız gereken:
x_(n+1) = x_n - (f'(x_n)/ f''(x_n)) (Tabii burada f fonksiyonunun iki kere türevlenebilir olması gerek)Yalnız, yordamı uygulama esnasında bir iki noktaya dikkat etmek gerekir. Şöyle ki:
- Başlama noktasını(ilk tahminimizi) iyi seçmeliyiz.Asıl kökten çok uzakta seçilen noktalar, yaklaşma işleminin başarısızlıkla sonuçlanmasına ve ilgisiz değerlere ulaşılmasına neden olabilir. Bu yüzden Newton Yordamı, daha çok yerel bir yöntem olarak düşünülür.
- Adımların herhangi birinde türevi sıfır olan bir noktaya rastlamak, bir sonraki adımı tanımsız kılacağı gibi türevi sıfır olmasa da sıfıra çok yakın olan noktalar, (normal bir sayının çok küçük bir sayıya bölümü çok büyük olacağından) bizi asıl kökten çok uzağa fırlatabilir.
- Bu yola başvurulması için f fonksiyonunun türevinin görece kolay bulunabilmesi gerekir. Türevini alması uzun ve sıkıntılı fonksiyonlar için, türevle alakası olmayan ve Newton Yordamı'ndan çok daha yavaş olan Secant Yordamı tercih edilir.
Bir de örnek
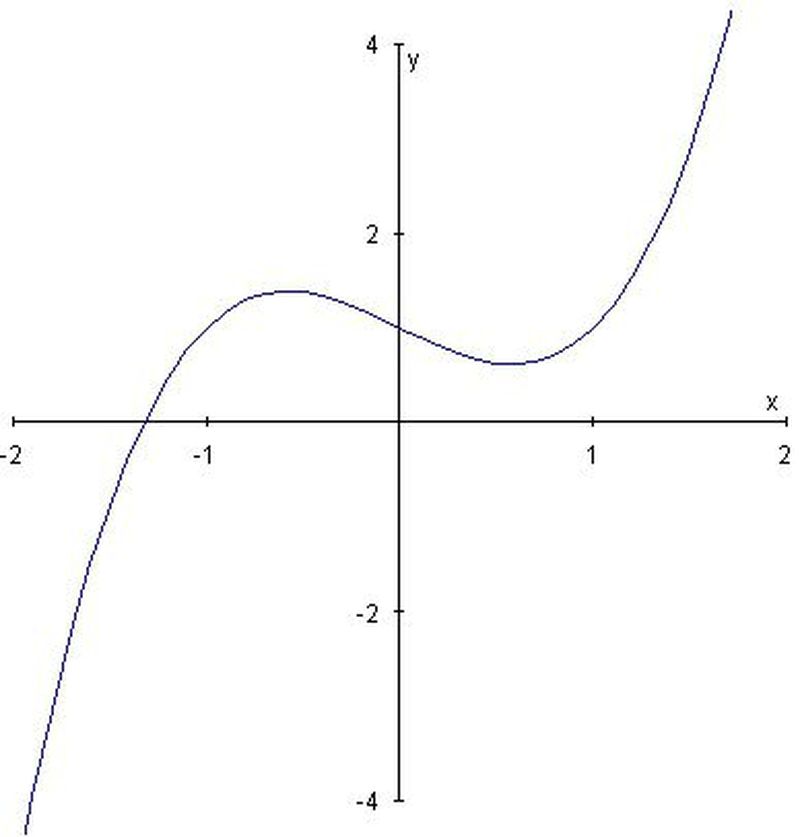
Sağdaki resimde gördüğümüz fonksiyonun kökünü bulmaya çalışalım. f, bir polinom fonksiyon olduğundan türevi kolaylıkla bulunabiliyor: f'(x) = 3x2-1
Kökün değeri için yapacağımız ilk tahminimizi ise -kökten çok uzak olmamasının gerekliliğini yukarıda belirttiğimizden- Ara Değer Kuramı'ndan (Intermediate Value Theorem) yararlanarak bulabiliriz.( Bu kuramın yardımıyla f(-2)= -5 ve f(-1)= 1 olduğundan denklemin [-2,-1] aralığında bir kökü bulunduğunu söyleyebiliriz ) Bunun sonucunda ilk tahminimiz x_0'a -1 değerini verirsek işin hesaplama kısmını programımız bizim için halledecek ve bu yordamla kök için elde edeceğimiz yaklaşık değerler sırasıyla şunlar olacaktır:
x_0 = -1
x_1 = -1.500000
x_2 = -1.347826
x_3 = -1.325200
x_4 = -1.324718
x_5 = -1.324717x_6 = -1.324717Gördüğünüz gibi henüz beşinci tahminimizde denklemin kökünü 10-6 hata payıyla bulmayı başardık.Hata payını kendi uygulamalarınızda dilediğiniz gibi küçültüp istediğiniz nitelikte sonuçları hızlı bir biçimde elde edebilirsiniz.
Umarım bu ilk teknik konulu yazımda sizlere Newton Yordamı ve kullanımları konusunda sizlere yeterince yardımcı olabilmişimdir.Artık 85. derecen denklemlerin kökünü bile ufacık bir hatayla da olsa rahatlıkla bulabilirsiniz! Gelecek ay görüşmek üzere:)