E-bergi'deki yazılarıma bir tek uçaktan seslenerek başlamamıştım sanırım, bu yazımda bu ilki de gerçekleştiriyorum ve bulutların üstünden selamlıyorum hepinizi! Malum dergimiz bir yaşına daha giriyor ve yazı yazmazsam olmaz diyerek kısacık da olsa her zamanı ayırmaya çalışıyorum. Bizi bu yıl da can-ı gönülden desteklediğiniz, destek mesajlarınızı esirgemediğiniz, yanlışlarımızı düzeltecek kadar ailemizden hissettiğiniz ve her sayımızı merakla ve heyecanla beklediğiniz için teşekkür ediyorum ve daha fazla uzatmadan bu ayki konumuza geçiyorum: Kameralar! Evet bu kadar basit, sizlere bu ay bilgisayar grafiği ve bilgisayarlı görme konularında çok önemli yer tutan kamera modellerinden bahsedeceğim. Sanal ortamdaki bu kamera modellerinin bazıları gerçek kameraları simüle etmeyi amaçlarken, bazıları ise sentetik dünyaya çok daha farklı bakış açıları getirerek normal kameralarla elde edemeyeceğimiz görüntüleri sağlamaktadırlar.
Kamera Derken?
Çoğumuzun fizik dersinden bildiği optik konuları aslında kamera denince aklımızda birşeyler canlanmasına yeter. Ancak bilgisayar grafiklerinde kamerayı biraz daha genel anlamda kullanabiliriz, bir yüzey ve o yüzeyden çıkan ışınlar aslında bir kamerayı tanımlamaya yeterlidir; ancak bir kameranın olmazsa olmazı görüntü düzlemini de unutmamak gerekir. Bu kavramları farklı kamera modelleri gördükçe parametrelere dayandırarak anlam kazandıracağız. Şimdi dilerseniz en bilinen (dikkat ettiyseniz en genel demiyorum) kamera modeliyle başlayalım; çünkü bu modeli oturtmadan diğer modelleri anlamak biraz daha kafa karıştırabilir.
İğne Deliği Kamera Modeli (Pinhole Camera Model)
Yine lise fiziğine dönelim, hani karanlık bir kutunun dışında bir mum vardi, kutuda da bir delik, sonra kutunun içindeki mum görüntüsü ters çıkardı, sanırım herkes hatırlamıştır :) Nesnenin köşelerinden çıkan ışınlar odaktan (kutudaki delikten) geçerek kutunun içinde karşılaştıkları ilk yüzeyde mumum görüntüsünü oluşturur. İşte iğne deliği kamera bu modelin aynısının bilgisayar grafiği alanına uygulanmışı. Tabi bazı farklarla. Hatırlarsanız mumun görüntüsü normalde kutunun içindeki ekranda veya yüzeyde oluşurdu. Grafikte ise çok daha basit bir yaklaşımımız var: aynı yüzeyin odakla nesne arasındaki simetriğini alarak, buna görüntü düzlemi (image plane) diyoruz. Böylece hem görüntü ters olusmamış oluyor, hem de mesafeler daha kontrol altında oluyor. Bu yeni durumda odak artık göze dönüşürken; göz, görüntü düzlemi ve nesneyi birleştiren eksene de optik eksen deniyor.
İğne deliği kameranın tek denklemi de bu optik eksen üzerinde bulduğumuz üçgenlerin benzerliğinden çıkardığımız bağıntıdan geliyor. Şekildeki gibi konuşlanmış bir iğne deliği kamera düzeneğinde, göz-görüntü düzlemi üzerindeki bir nokta-görüntü düzleminin optik ekseni kestiği nokta üçgeni ilk üçgenimiz olsun. Aynı şekilde göz-görüntü düzlemindeki noktanın nesnenin üzerinde denk geldiği nokta-nesnenin bulunduğu düzlemin optik ekseni kestiği nokta üçgeni de ikinci üçgenimiz olsun. Şekilden de belli olduğu gibi bu iki üçgen benzerdir ve aralarındaki bağıntıları şöyle yazabiliriz: y/f=Y/Z=taban/optik eksen üzerindeki kenar. Aynı şekilde x ekseni için de denklemi yazdıktan sonra, üç boyutlu dünyamızda yerini bildiğimiz bir noktanın görüntü düzlemindeki karşılığını bulabilmek sadece bu denklemleri x=f*X/Z ve y=f*Y/Z şeklinde yazarak o noktanın koordinatlarını bulmaya kalıyor. Bu işlemin hepsine de perspektif izdüşüm (perspective projection) deniyor.
Perspektif Kamera Parametreleri
Bu kameraları işlemlerle tanımlayabilmek ve bütün görüntü dönüştürme işlemlerini matrislerle halledebilmemiz için kameraları matematiksel olarak tanımlayabilmemiz gerekiyor. Bir kameranın durumunu belirleyen bu parametreler içkin (intrinsic) ve dışsal (extrinsic) olarak ikiye ayrılıyor.
İçkin Parametreler:
Bu özellikler kameranın öntanımlı özellikleri değildirler. Kameradan kameraya (ve modelden modele) değişir. Aynı kamera için farklı değerler almaları da çok nadiren mümkündür (zooming veya farklı lens takma, vb.). Tek tek incelersek:
f, Odak uzunluğu (focal length): En önemli içkin parametredir çünkü görüş alanını belirler. Yukarıdaki denklemde kullandığımız f'e denk gelir. p_x, p_y, Esas nokta (principal point): Genelde görüntü düzleminin orta noktası olarak kabul edilir. Aslında optik eksenin görüntü düzlemini kestiği noktadır; dolayısıyla görüntü düzlemini farklı konumlandıran kamera modellerinde değişebilir. s_x, s_y, Piksel boyutu (pixel size): Günlük kameralarda pikseller kare olmak zorunda değildir ve boyutları belli herhangi dörtgenler olabilir; işte bu boyutları bu parametre belirler. Bilgisayar grafiğinde tanımlanan kameralarda ise genelde kullanılmayan bir parametre olarak 1 kabul edilir. k_1, ... Bozulma katsayıları (distortion coefficients): Çeşitli nedenlerden dolayı (lens özellikleri, aynalı bir kamerasa ayna kullanımı, vs.) görüntüde yaşanan bozulmayı temsil eden katsayılardır. Bu katsayıların görüntüleri çeşitli matrislerle ifade ettikten sonra bulunması mümkündür ancak şu an bu basit sentetik modeliminz için bu katsayıları sıfır olarak kabul ediyoruz (kodumuz böcekli değilse :) )
Dışsal parametreler:
İçkin parametrelerin aksine sürekli değişirler :) Basit olarak kameranın dünya ile etkileşimini sağlarlar. Yön (rotation): Kameranın baktığı yeri belirler, üç ayrı değer vardır. Kamerayı üç boyutlu koordinat sisteminde düşünürsek, x ekseni etrafında dönmesine yaw, y ekseni etrafında dönmesine pitch, ve z ekseni etrafında dönmesine ise roll denir. Farkına kolayca varabileceğiniz gibi yaw ve pitch durumlarında kameranın baktığı nokta değişirken, roll durumunda baktığı nokta değişmez, sadece yukarı vektörü değişir. Konum (translation): Yine kameramızı üç boyutlu dünyada düşündüğümüzde x, y ve z eksenlerine göre yeri kameranın konumudur.
Bir Kamerayı Matematiksel Olarak İfade Etmek
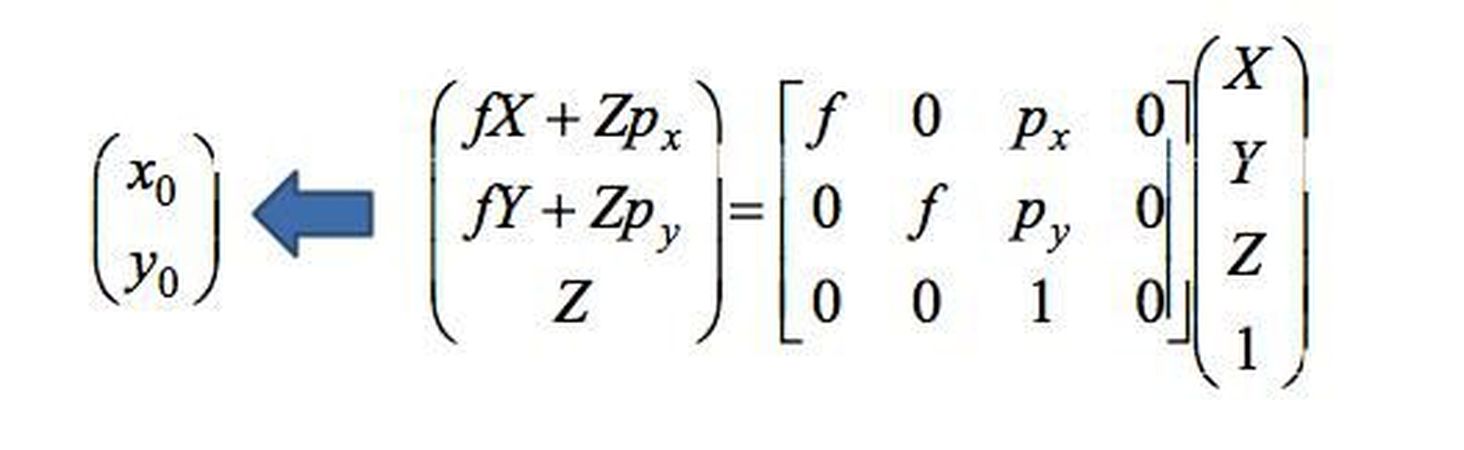
Kameranın özelliklerini parametrize edebildik, şimdi bunlar arasındaki bağıntıyı bulalım. Baştaki perspektif izdüşüm formülümüze geri dönersek, görüntü düzlemi üzerindeki noktayı biraz daha farklı gösterelim: homojen koordinatları hatırlıyor muyuz? Hatırlamıyorsak detaya girmiyorum ama bu gösterinin oradan geldiğini bilirseniz araştırmanız daha kolay olur. Bundan sonra tüm işlemlerimizi homojen gösterim üzerinden yapacağız, yani üç boyutlu noktalarımız dört elemanlı birer vektör, iki boyutlu elemanlarımız ise üç elemanlı birer vektör olacak. Bir kameranın yaptığı işlem üç boyutlu noktayı alıp iki boyutlu görüntü düzlemindeki izini bulmaksa, kamera denklemimizin 3x4 boyutunda olduğunu bulmamız çok kolay. Şimdi içeriğine bakalım.
Üstteki şekilde görüldüğü gibi, artık x,y noktalarımızı elde etmek için ufak bir basamağımız daha var arada, homojen gösterimden dönüştürmek olarak düşünebilirsiniz. Bu şekilde gösterdiğimizde en baştaki perskpektif izdüşüm işleminin eşitliğin sağındaki matristen hiçbir farkı yok! Demek ki ilk içkin parametremizi kamera matrisimize yerleştirdik. Gelelim kameranın esas noktasina, orijinine. Eğer (0,0) almazsak, yapmamız gereken sadece modelimizi o noktaya taşımak değil mi? Bu yüzden eşitliğin solundaki gibi sadece bir taşıma işlemi ekliyoruz matrisimize.
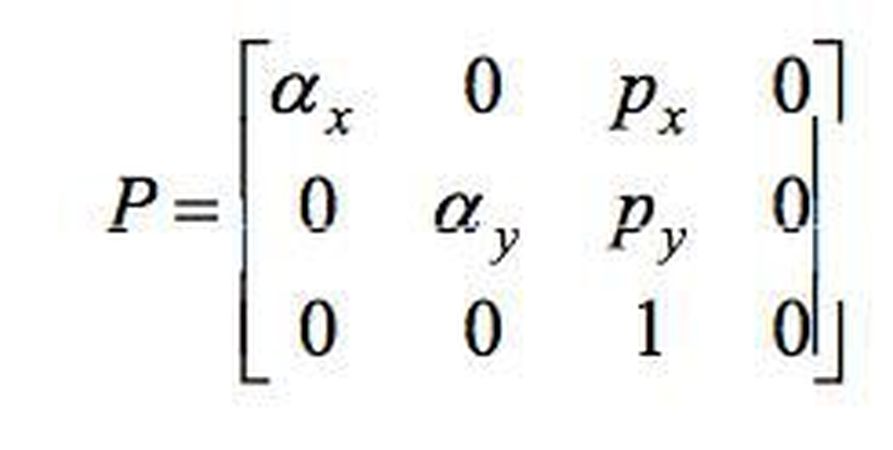
Hatırlarsanız odak uzunluğumuz aslında bir benzerlikten geliyordu ve bunu diagonalde bir çarpma olarak, yani aslında bir ölçekleme olarak ifade etmiştik. Şimdi piksel boyutlarımızı da aynı şekilde ifade edeceğiz. Eğer öntanımlı olan (1,1) değerlerini almıyorsak, x ve y eksenlerinde yapacağımız ölçekleme yine bu değerleri koyduğumuz bir matristen başka bir şey değil. Bu matrisi önceki matrisimizle çarptığımızda ise soldaki genel matrisi elde ediyoruz. Burada a_x=s_x*f, a_y=s_y*f olarak çarpılmış halini görüyoruz. Bozulma katsayılarına gelirsek, bunlar bu matrise herhangi bir işlemin uygulanması ile elde edilebilir. Genel bazı bozulmalar vardır, ancak bunlara şimdilik değinmeyeceğiz. Dolayısıyla içkin parametrelerimizin hepsini yerleştirdik, bu matrisimize P diyoruz ve dışsal parametreler ile devam ediyoruz.
Bir an kameraları unutup geometriye dönelim. Eminim diğer grafik ve/veya bilgisayarlı görme konulu yazılarımızda üç boyutlu koordinat sistemlerinde dönme ve ötelemenin nasıl gerçekleştirildiğini belirtmişizdir; o yüzden hızlı geçeceğim. Öteleme ile başlayalım, kameranın esas noktasında yaptığımız gibi, sırasıyla x, y ve z eksenlerindeki öteleme miktarını içeren öteleme vektörünü üçüncü sütuna yerleştireceğiz ve dünyadan-kameraya dönüşüm matrisimizin öteleme kısmı tamamlanacak.

Dönmelere gelirsek, yaw, pitch ve roll değerlerinin herbiri için ayrı birer matrisimiz var. R_x, R_y ve R_z ile gösterdiğimiz bu matrisleri yazarasak soldaki gibi üç matris elde ederiz. Bu matrisleri çarpıp (hangi sırayla çarpıldıkları önemli değil çünkü bu matrisler orthonormaldirler) bir dönme matrisi edindiğimizde (R diyelim), bunu genel dünyadan-kameraya dönüşüm matrisimize şu şekilde uyguluyoruz: ilk 3x3'lük kısmını alıp, genel dünyadan kameraya dönüşüm matrisimizin 3x3'lük kısmı olarak kullanıyoruz. E öteleme vektörümüzü de zaten koymuştuk, gerisini de sıfırla doldurduktan sonra dışsal parametrelerimizin kullanıldığı matris hazır! Bu matrisi bundan sonra M olarak çağıracağız.
'Kamerayı Anladık, Kodu Göster!'
Kameramızın bütün parametrelerini yerleştirdiğimize göre geriye kalan tek şey bu iki matrisi çarpıp üç boyutlu noktaya uygulamak. Kısaca homojen gösterimdeki noktamız görüntü noktamız k ile üç boyutlu noktamız K arasındaki bağıntı: k=P*M*K, bu kadar basit. Artık üç boyutlu noktamızı gören bir kameramız var. Bu kamera setupını OpenGL ile kurmak istersek aşağıdaki kod parçasını kullanabiliriz:
glMatrixMode(GL_PROJECTION);
gluPerspective(görüş açısı, 1.0, yakın düzlem, uzak düzlem);
glMatrixMode(GL_MODELVIEW);
glTranslatef(tx,ty,tz); // taşınacak nokta (tx,ty,tz) ise
glRotatef(rx,1,0,0); // x ekseni etrafında rx derece döndük
glRotatef(ry,0,1,0); // y ekseni etrafında ry derece döndük
glRotatef(rz,0,0,1); // z ekseni etrafında rz derece döndükBurada bütün parametreleri istediğiniz gibi kullanamıyorsanız kendi P*M matrisinizi oluşturup şu şekilde yükleyebilirsiniz:
glLoadMatrixf(matris);Daha ayrıntılı kamera modellerine daha sonraki yazılarda değineceğiz ve bunların OpenGL ile gösterimlerinde bu parametrelerin daha ayrıntılı açıklamasını vereceğiz ancak basitçe gluPerspective fonksiyonu içkin parametreleri yüklerken, glTranslate fonksiyonu ötelemeyi halleder ve glRotate fonksiyonları da aldıkları eksenlere göre dönmeyi ayarlar. Bu arada kafanızda soru işareti kaldıysa, OpenGL'de matris çarpımlarının ters olduğunu hatırlatarak, o yüzden bu sırayla yazdığımızı vurgulamak istiyorum.
Sanırım başlangıç için yeteri kadar yol gösterici bir yazı oldu, umarım aradığınızı bulabilmişssinizdir. Gelecek aylarda kamera modelleri ile devam ederek genel lineer kamera ile fantastik görüntüler oluşturup, occlusion resistant kamera ile nesneleri kısmen hayaletleştirebileceğiz! :) O zamana kadar, mutlu yıllar e-bergi, neşeli kutlamalar topluluk ve eğlenceli okumalar sevgili okurlarımız :)