Merhabalar,
E-bergimizin bu yazısında, sizlere ikilik sayma sisteminden ve bu sistemin bilgisayarlar tarafından kullanımı sürecindeki toplama, çıkarma, çarpma işlemlerinin uygulanışından bahsedeceğiz.
İkilik sayma sistemi, diğer bir adıyla ikilik taban, sayıların yalnızca iki rakam kullanılarak ifade edildiği ve matematiksel işlemlerin bu gösterimler üzerinden yapıldığı bir sayma sistemidir. Bu sistem, mantıksal kapıların kullanıldığı elektrik devrelerine uygunluğundan dolayı modern bilgisayarlarda kullanılmaktadır. Sayıları ifade etmek için kullanılan bu iki rakam geleneksel olarak 1 ve 0'dır. Ancak 1 ve 0 tek seçenek değildir. Onların yerine farklı semboller (+ ve - gibi) ya da farklı durumlar (beyaz ve siyah) da seçilebilir. Bilgisayarın iç yapısında kullanılan ikilik sistemde ise bu 1 ve 0 yerine elektriğin (ya da akımın) varlığı ve yokluğu kullanılır. Bizler için 1 elektriğin varlığını, 0 ise elektriğin olmadığı (ya da belirli bir seviyenin altında olduğu) durumları temsil eder. İkilik sayma sistemi hakkında daha detaylı bilgi için E-bergi'nin Eylül 2009 sayısında Üstün Yıldırım'ın "İkilik Sistemler" adlı yazısına başvurabilirsiniz.
İşaret Biti
Pozitif sayıların bilgisayarda gösterimi ikilik sistemin yaygın kullanımdaki gibi olmakla birlikte, negatif sayılar için durum bir miktar daha karmaşıktır. Genel matematikte bir sayının negatifliği ifade etmek için kullanıdığımız "-" bilgisayarda kullanılamamaktadır. Bu sorunun en basit çözümü her sayının en sol bitinin işaret biti olarak kullanılmasıdır. Bu bitte bulunan 0 sayının pozitif olduğunu gösterirken, 1 bu sayının negatif olduğu anlamına gelir. 1 baytlık (8 bitlik) bir sayıyı inceleyelim. Sayımız 10010110 olsun. İşaret biti, yani en sol bit, 1 olduğu için sayımız negatif. Diğer 7 hane de bize sayımızın mutlak değeri hakkında bilgi verir. 2lik tabandaki 0010110 sayısı, onluk tabanda 22ye karşılık geliyor. O halde, 10010110 sayısı bilgisayarımız için -22'yi temsil ediyor.
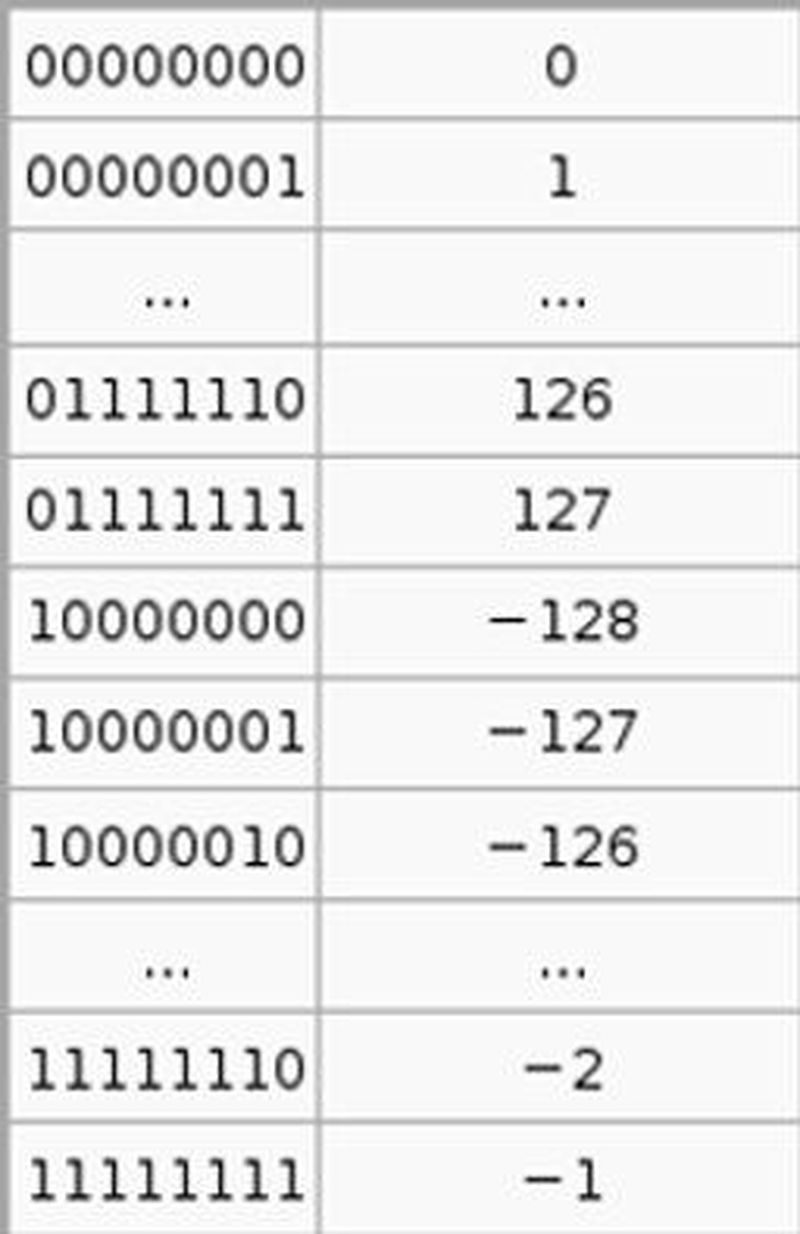
Bir işaret biti eklemek yöntemi bizim için oldukça basit bir yöntem olmasına karşın, bilgisayarlar için en kullanışlısı olmayabilir. Öncelikle bizi 0'ın iki farklı ifade şekliyle karşılaştırır ki bu durum bilgisayar için +0 ve -0'ın iki farklı sayı olarak algılanmasına sebep olur. Bu yöntemin dezavantajlarından bir diğeri de bilgisayarın her toplama/çıkarma işlemi yapışından önce elindeki sayıların işaretini kontrol etmesi gerekmesidir. Bu iki işlemin bilgisayarın en sık yaptığı işlemlerden olduğu göz önünde bulundurulduğunda bu gösterimin alternatiflerinin düşünülmesi kaçınılmaz olur. Sıklıkla kullanılan bir alternatifi "ikiye tümleyen"dir.
İkiye Tümleyen
İkiye tümleyen yönteminde de pozitif sayıların gösterimi aynıdır ve en sol bite bakarak sayının işareti hakkında yorum yapılabilir. Ancak bu bite işaret biti demek doğru değildir; çünkü en sol bitte bulunan 1, yalnızca sayının işaretini belirtmekle kalmayıp sayının değerini de etkiler. n-bitlik bir gösterimin en solundaki 1 rakamı, sonraki bitlerin belirttiği sayıdan çıkarılacak 2<sup>(n-1)</sup>lik bir değer olarak da algılanabilir.
Negatif bir sayının 2ye tümleyendeki gösterimini bulmanın en pratik yolu şu şekildedir: Sayı en sağ bitten başlanarak incelenir. En sağdaki 1e kadar olan 0lar aynen bırakılır. İlk 1 de olduğu gibi kalır, daha sonraki tüm 0lar 1e, tüm 1ler 0a çevrilir. Böylelikle tüm pozitif sayıların ikiye tümleyeninin en sol işareti 1 olurken, sıfır sayısının işareti aynı kalır. Örnek olarak, 00101100 sayısının (10luk sistemde 44) tümleyenini alalım. En sağdaki 1, sağdan 3. bitte olduğu olduğu için sağdaki 3 biti aynen bırakıyoruz, daha sonraki tüm rakamları değiştiriyoruz. O halde bu yöntemle 44ün tümleyeni, yani -44, 11010100 oluyor. Eğer elde ettiğimiz sayının tekrar tümleyenini alınırsa bunun 00101100 (10luk sistemde 44) olduğu gözlemlenir. Bu örnekte de görüldüğü gibi, her sayının tümleyeninin tümleyeni kendisini verir.

Bu yöntemle bir negatif ve bir pozitif sayının toplanması sırasında uygulanan işlem iki pozitif sayının toplanmasıyla aynıdır. Fazladan bir kontrol ya da farklı bir yol uygulanmaz. En sol basamaktaki rakamları toplamı bize bir elde verdiğinde, bu elde yok sayılır. Örnek bir durum soldaki resimde gösterilmektedir. -1 ile 3'ün toplanması sırasında en sol bitlerden bir elde gelir. Bu elde ihmal edildiğinde doğru sonuca ulaşılmış olunur.
İkiye tümleyen bilgisayardaki çıkarma işlemlerinde de kullanılır. Bilgisayarlarda ayrıca bir çıkarma devresi bulunmaz ve çıkarma işleminin sonucu, çıkanın tümleyeni ile çıkarılanın toplanmasıyla bulunur. Bir diğer deyişle, bilgisayarlar için A sayısından B sayısını çıkarmak, A sayısına B sayısının ikiye tümleyenini eklemek anlamına gelmektedir.
Çarpma
İşaret bitili gösterimler için kullanılan çarpma yöntemlerini hiç bir uyarlama yapmadan ikiye tümleyenli sistemlerde kullanmak mümkün değildir. Bunun için iki farklı yöntem uygulanır. İlkinde, eğer 2.çarpan negatifse iki çarpanın da tümleyeni alınır. Böylece sonucu etkilemeden 2. çarpan pozitif yapılmış olur. 2. çarpanın pozitif olduğu durumlar ikilik sistemin standard çarpma işlemi uygulanır.
İkinci yöntemi gözünüzde ekle-kaydır algoritması gibi canlandırabilirsiniz. Ancak kağıt ve kalemle yaptığımızdan biraz farklı. Kısmi çarpımları sola kaydırmak yerine, elde ettiğimiz kısmi çarpım toplamları her basamakta bir birim sağa kaydırılır. Böylece elimizdeki ara sonucun en sol basamağı bir sonraki yazmaça (register) kaydırılmış olur. Unutulmaması gereken önemli bir nokta bu yöntemin kullanımında ilk yapılması gereken şeyin ilk çarpanın başına fazladan bir işaret biti eklenmesi gerektiğdir. 6 ile -5'in bu yöntem kullanılarak çarpılışını aşağıdaki örnekte inceleyelim. (Sonradan eklenmiş olan işaret biti ve iki yazmaç "|" işaretleri ile ayrılmıştır)
0 0110 (6) (1\. çarpan, başında bir işaret biti ekli)
× 1011 (-5) (2\. çarpan)
= |==== | ===
0 | 0110 | 0000 (ilk kısmi çarpım (2\. çarpanın en sağ biti ile 1\. çarpanın çarpımı))
0 | 0011 | 0000 (ek işaret biti korunarak sağa kaydırıldı.)
0 | 1001 | 0000 (ikinci kısmi çarpım eklendi.)
0 | 0100 | 1000 (ek işaret biti korunarak sağa kaydırıldı.)
0 | 0100 | 1000 (üçüncü kısmi çarpım (0) eklendi.)
0 | 0010 | 0100 (ek işaret biti korunarak sağa kaydırıldı.)
1 | 1100 | 0100 (son kısmi çarpım elimizdeki sayıdan çıkarıldı.)
1 | 1110 | 0010 (ek işaret biti korunarak sağa kaydırıldı.)
| 1110 | 0010 (ek işaret biti yok sayılarak sonuç -30 olarak bulundu.)Taşma
Yazımı sonlandırmadan önce bahsetmem gereken önemli bir nokta taşma proplemi. Unutulmamalı ki bilgisayarın belirli alanda tutabileceği sayıların bir alt limiti ve de bir üst limiti vardır. Örneğin, 1 baytta (8 bitte) ikiye tümleyen olarak tutulabilecek en büyük sayı 01111111 (127) ve en küçük sayı 10000000 (-128)dır. Limitlerin dışında kalan sayılar bu alanda tutulmaya çalışıldığında sorunlarla karşılaşılması beklenen bir sonuçtur. 1 baytlık hafızada tuttuğumuz 01100101 (101) sayısı ile 00011100 (28) sayısını toplamak istediğimizde bilgisayarın bize vereceği yanıt 10000001 (-127) olacaktır ve bu açıkça görüldüğü üzere yanlış bir sonuçtur. Hafızada tutulmak istenen sayının tutulabilecek sayı limitlerinin dışında kalmasından kaynaklanan bu ve benzeri sorunlar taşma olarak adlandırılır.
İkiye tümleyen kullanıldığında aynı işaretli sayıları toplarken bu istenmeyen durum oluşabilir ve sorun sonucun işaret bitinin kontrol edilmesiyle saptanabilir. Pozitif sayıların toplamının negatif veya negatif sayıların toplamının pozitif olması taşma olduğunun göstergesidir. Taşma ihtimalinin epey yüksek olduğu çarpma işleminde ise sonucun tutulduğu yazmaçın büyüklüğü iki katına çıkarıldığında bu ihtimalden kesin olarak kaçılmış olunur.
E-bergimizdeki bu ilk yazımda sizlere ikiye tümleyen ve toplama/çarpma işlemlerindeki uygulamaları hakkında elimden geldiğince bilgi vermeye çalıştım. Umarım faydalı olabilmişimdir. Önümüzdeki sayılarda buluşmak üzere hoşçakalın, mutlu kalın.