Bilgisayarlar geliştikçe artık günümüzde birçok işlem çok hızlı yapılabiliyor. İnsanların günlerini verip de yapamayacağı problemleri hızla çözebiliyor. Acaba bilgisayarların da çözemeyeceği problemler var mıdır ya da her problemi bilgisayarlar bizim kabul edebileceğimiz hızda çözebilir mi? Mesela, Hanoi kulelerini herkes bilir. 3 çubuk ve farklı boyutlardaki halkalardan oluşan ve halkaları, büyük olan halkalar kendinden küçük olan halkaların üstüne hiçbir zaman gelmeyecek şekilde bir çubuktan diğerine aktarma oyunu. Bu problemi her işlemi 1 ns’de yapan bilgisayara şimdiye kadar bilinen en hızla algoritmayla, O(2<sup>n</sup>) bilgisayara yaptırmak istesek ne olurdu?
Normalde bizler 100,000 halkalı Hanoi Kulesini çözmeye gerek duymayabiliriz ama yine benzer karmaşıklıktaki bir problem bizim için çok önemli olabilir ve 100,000 hiç de büyük bir sayı değil.
Bilgisayar biliminde çözülmeyi bekleyen ama kabul edilebilecek sürede çözülemeyen birçok problem bulunmakta. Bunlardan birkaçını tanımlamak gerekirse:
- Bir çizgede (graph) belirli bir sayıda düğüm içeren ve içerdiği tüm düğümler birbirine bağlı olan alt çizgeler bulunabilir mi? (Clique Problem)
- Bir çizgedeki tüm düğümleri en az sayıda kenar ile bağlayabilen bir yol kümesi bulunabilir mi? (Vertex-cover Problem)
- Bir çizgede tüm düğümlerden bir ve yalnız bir kere geçen ve yeniden başladığı düğüme geri dönen bir yol bulunabilir mi? ( Hamiltonian Cycle Problem)
- Bir çizgede bir yol ile bağlı olan düğümlerin renkleri farklı olacak şekilde en az kaç renkle boyayabiliriz? (K-Coloring of Graph)
İşte bu problemler bilgisayar dünyasını meşgul ediyor ve hatta bunlardan birini çözene yüklü miktarda para vaat ediliyor. Bu yazımda sizlere bu problemlerin nasıl problemler olduklarını ve hangi grupta incelenmeleri gerektiğini anlatmaya çalışacağım.
Konumuza girmeden önce bazı tanımlamalar yapalım. Hesaplama teorisi (Theory of computation) bilgisayar biliminin bir problemin belirli bir algoritma ve hesap modeli ile çözülüp çözülemeyeceğini veya çözülürse ne kadar hızlı ve verimli bir şekilde çözüleceğini inceleyen bilim dalıdır. Başlıca 2 dala ayrılır: karmaşıklık teorisi (complexity theory) ve hesaplanabilirlik teorisi (computability theory). Karmaşıklık teorisi genelde karar verme problemleri (decision problems) ile uğraşır. Karar verme problemi sorulan bir soruya evet ya da hayır olarak cevap verebilme ile ilgilidir. Mesela, verilen herhangi bir sayı için “asal mı” (IS-PRIME) sorusuna evet ya da hayır olarak cevap verebilme problemi bir karar verme problemidir. Bu tip problemler özellikle incelenmektedir çünkü herhangi bir problem bir karar verme problemine indirgenebilir ve bu sayede çözüme ulaştırılabilir. Örneğin; “çarpanı var mı” (HAS-FACTOR) problemi bir sayının yine verilen bir sayıdan küçük asal çarpanı olup olmadığı sorusuna cevap verir. Bu problemi çözebilirsek verilen herhangi bir sayının asal çarpanlarını bulma sorununa da aynı zamanda çözmüş oluruz.
Hesaplama karmaşıklığı teorisi (computational complexity theory) bilgisayar biliminde hesaplama teorisinin bir alt dalı olarak sınıflandırılır. Bir algoritmanın bir problem üzerinde çalıştırılması durumunda ne kadar kaynağa gereksinim olduğunu inceleyen bilim dalıdır. Bu teori, bir girdinin büyüklüğü artırıldığında buna bağlı olarak algoritmanın çalışma zamanının ve hafıza ihtiyaçlarının ne kadar arttığını araştırır. Algoritmaların karmaşıklığı genelde zamanla bağlantılı olarak ölçülür ve büyük O (big O notation) ile ifade edilir. Örneğin O(n), O(n<sup>2</sup>) sırasıyla n büyüklüğündeki bir veri girildiğinde bu algoritmanın yavaşlığının o girdinin büyüklüğüyle doğru orantılı olarak arttığını gösterirken, n<sup>2</sup> olan ise bu girdinin büyüklüğünün karesiyle doğru orantılı olarak değiştiğini gösterir.
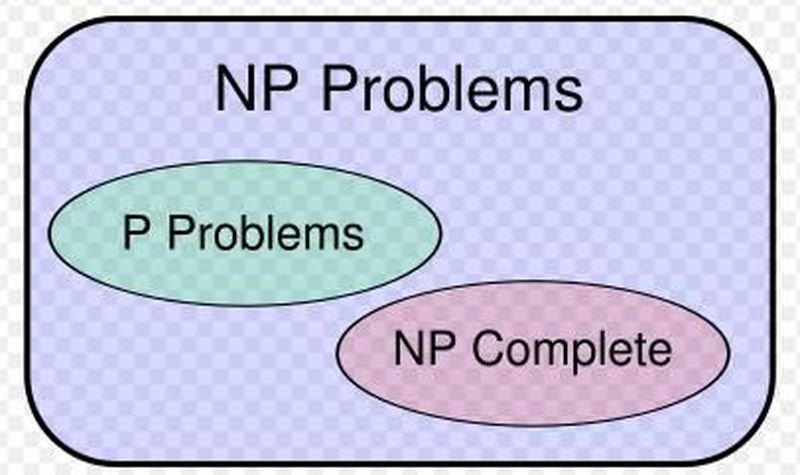
Bu tanımlar biraz sıkıcı olmuş olabilir ama şimdi bu tanımlardan yola çıkarak asıl konumuza geleceğiz. Karmaşıklık teorisinde problemler çözülebildikleri en hızlı karmaşıklığa göre karmaşıklık sınıflarına (computational complexity) ayrılırlar. Bunlardan en önemlileri P (deterministically polynomial, deterministik polinomsal) ve NP(non- deterministically polynomial- deterministik olmayan polinomsal)’ dir. P kategorisine giren problemler karmaşıklığı O(n<sup>k</sup>), k ∈ R ile ifade edilebilen ve deterministik Turing makinesinde polinomsal zamanda çözülebilen problemlerdir. Örneğin; en büyük ortak bölen bulma ya da sıralı bir liste içinde arama yapma polinomsal zamanda çözülebilir ve bu yüzden P sınıfı problemlerdir.
NP problemler ise en büyük karmaşıklık sınıflarından birini oluşturur. Hatta P sınıfı da NP sınıfının içinde gösterilir. NP problemler deterministik olmayan Turing makinesiyle polinomsal zamanda çözülebilirler. Günümüzde deterministik olmayan bir Turing makinesi bulunmadığından NP problemler için verimli kabul edilebilecek bir algoritma bulunamamıştır. Örneğin; 2 çizgenin (graph) izomorfik olup olmadığının hesaplanması yani 2 çizgenin aynı şekli oluşturacak şekilde çizilip çizilemeyeceğinin hesaplanması polinomsal zamanda yapılamamaktadır.
NP sınıfına dâhil olan problemlerin bazıları o kadar zordur ki bunlara polinomsal zaman bulmak teşebbüsleri çok uzun uğraşlardan sonra sonuçsuz kalmıştır. Bu sınıfa NP-Complete adı verilir. Bir problemin NP-Complete (NPC) sınıfında olduğu kabul edilmişse o problem için polinomsal zaman bulunmasının çok zor olduğu anlaşılabilir.
Yollardan beri NP sınıfı içindeki problemler çözülmeye çalışılmıştır ancak çok azı dışında bu başarılamamıştır. İlerlemeler ise umut vericidir. NPC problemlerin herhangi biri polinomsal zamanda çözülebilirse, NP sınıfındaki tüm problemlerin de polinomsal zamanda çözülebileceğini ispatlayan bir makale yayınlanmış ve tabi ki bununla da bilgisayar biliminde çok büyük bir devrim gerçekleşmiştir. 1971 yılında bir bilgisayar bilimci olan Stephen Cook “The complexity of theorem proving procedures” adlı bilimsel yazısında bugün Cook teoremi olarak bilinen bir teoremi ispatlamıştır. Bu teoremde “Mantıksal Sağlanabilirlik” probleminin (Boolean satisfiability Problem) NP-Complete olduğunu göstermiştir. Biraz daha açıklamak gerekirse NP sınıfındaki herhangi bir problem polinomsal zamanda deterministik Turing makinesi tarafından bir mantıksal formülünün sağlanabilir olup olmadığı problemine indirgenebilir. Bu teoremin bize sağladığı en büyük yarar ise; eğer mantıksal sağlanabilirlik problemine deterministik ve polinomik bir çözüm bulunursa, NP deki tüm problemlerin de aynı şekilde çözülebileceğini ispatlamış olmasıdır. Aynı şey elbette PC olan tüm problemler için de geçerlidir. Bu sorun “P=NP?” sorunu olarak bilinir ve literatürdeki en ünlü ve en önemli problemdir. Hatta Clay Matematik Enstitüsü herhangi bir NPC problemini çözene 1 milyon $ vaat etmektedir.
Bir problemin çözülmesiyle diğerlerinin de çözülecek olması kulağa garip gelebilir çünkü sonuçta hepsi ayrı ayrı problemlerdir. Ancak bu problemlerin birbirine indirgeniyor olması diğerinin de aynı şekilde çözülebileceğini gösterir. İndirgeme işlemi aynı zamanda bir problemin NPC olduğunun da ispatıdır.
Bu ispatın yapılması 4 aşamada olur:
- NPC olduğu ispatlanacak olan problemin önce NP olduğunu gösterilir. Bunun yapılması için de deterministik olmayan, hayali bir makinede çalışan kod ile çözüldüğü gösterilir.
- Bilinen bir NPC problem seçilir.
- Sonra NPC olduğu bilinen problemin tüm durumları ispatlanmak istenen problemle eşleştirilir (reduction). Yani biri için doğru olan durum diğeri için de doğru olur.
- 3. maddedeki işlemin polinomsal zamanda yapıldığı gösterilir.
Yukarıdaki işlemlerin yaparak gösterdiğimiz şey; önceden NPC olduğunu bildiğimiz bir problemi polinomsal zamanda çözebilirsek diğerini de yine polinomsal zamanda çözebileceğimizdir çünkü birini diğerine indirgeme işlemi de polinomsal zamanda gerçekleşmiştir. Şimdi bir problemin NPC olduğunun nasıl ispatlandığını bir örnek üzerinde inceleyelim:
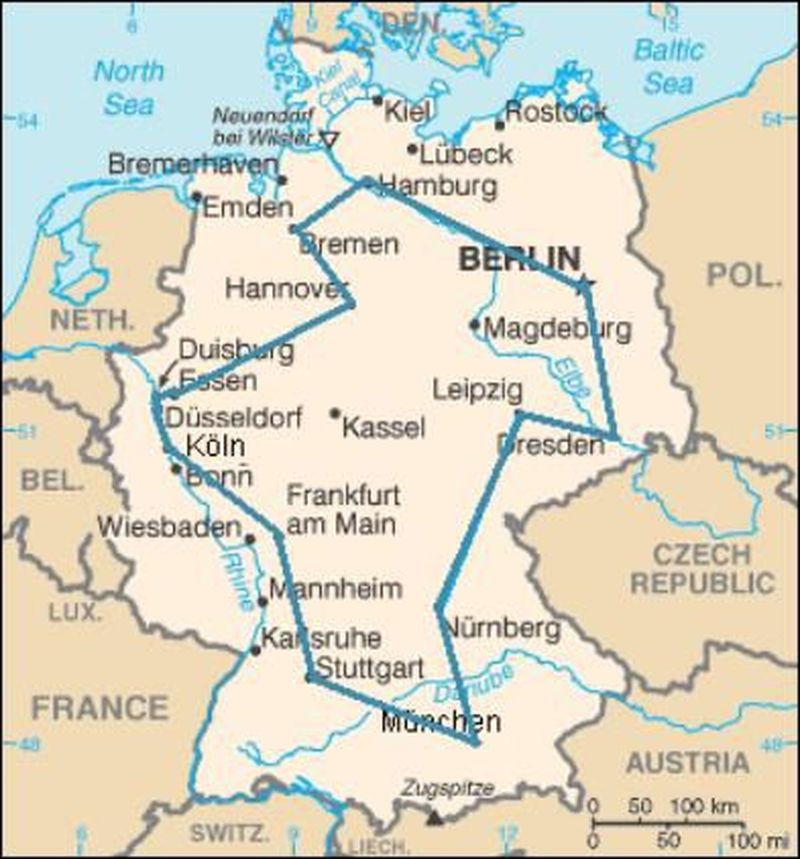
NPC olduğunu ispat etmek istediğimiz problem seyyar satıcı problemi (travelling-salesman problem,TSP) olsun. Bu problem, elindeki malları, bilenen bir çizgede en az masrafla tüm şehirlere 1 defa uğrayarak satmak isteyen birinin nasıl bir yol izlemesi gerektiği ile alakalıdır.
NPC olduğu bilinen problemimiz ise Hamiltonian Döngüsü Problemi (Hamiltonian Cycle-HCP) olsun. HCP, verilen herhangi bir yönsüz ve bağlı çizgede (complete undirected graph) tüm düğümlerden yalnızca bir kere geçerek başladığı yere geri dönen bir yol olup olmadığının bulunmasıyla ilgili bir problemdir. Bu problemin NPC olduğu Cook’un ispat ettiği mantıksal sağlanabilirlik probleminden yola çıkarak ispatlanmıştır. Biz de polinomsal zamanda çözülmüş olduğunu varsayarak yola çıkacağız. Kısaca, bizim Hamiltonian döngüsünün en az masraflı olanını bulmamız gerekmektedir. Şimdi bunu yukarıda bahsettiğimiz gibi 4 adımda yapalım:
- TSP NP sınıfına aittir.
Farz edelim ki, deterministik olmayan makinemizin tüm düğümleri geziyor ve gezerken de her zaman doğru ve en iyi yolu seçiyor. Normalde deterministik olmayan makineler bunu başaramaz ama bu makine en az masraf çıkaracak, başladığı yerde bitecek ve her düğümden 1 kere geçecek yolda kendiliğinden ilerleyebiliyor. Bu işlemin polinomsal zamanda gerçekleştiğini kabul ettiğimizden işlem yeterince hızlı bitiyor. Sonra elimizde olan yolun doğru olup olmadığını kontrol etmek için içinde geçen tüm düğümlerden bir ve yalnızca bir kere geçildiğini kontrol ediyoruz. Aynı zamanda da bu yolu kullanırsa ne kadar masraf edeceğini hesaplıyoruz. Eğer masraf belirli bir k sayısını geçmiyorsa programımız duruyor ve olumlu yanıt veriyor. Eğer yoksa olumsuz yanıt da verebiliyor. Kontroller elbette polinomsal zamanda bitiyor çünkü tüm düğümlerden yalnızca 1 defa geçiliyor (O(V)). Böylece TSP ‘yi deterministik olmayan makinede çözerek NP olduğunu ispatlamış oluyoruz.
- Hamiltonian döngüsü probleminin NPC olduğunu biliyoruz ve ispatlamak için onu seçiyoruz.
- HCP ile TSP ‘nin durumlarını eşleştiriyoruz. Böylece HCP’yi TSP’ye indirgiyoruz.
Farz edelim ki, elimizde bir Hamiltonian döngüsü barındıran G(V,E) çizgesi var (V düğümleri, E ise aralarındaki yolları gösteriyor). Bu çizgeden yola çıkarak ikinci bir G’(V,E’) çizgesi oluşturuyoruz. Oluştururken düğümler aynı kalıyor. Tüm düğümleri birbirine yollar ile bağlıyoruz. Ancak düğümleri yollar ile birbirine bağlarken G’de bulunan ve aynı zamanda Hamilton döngüsünün üstünde bulunan yolların masrafını 0 olarak belirlerken, diğer yollarınkini 1 olarak belirliyoruz. G çizgesi zaten yönsüz bir çizge olduğundan bir düğümden kendisine olan yollar G de bulunmuyor ve G’ de 1 olarak gözüküyor. Yeni oluşan çizgede masrafı 0 olan yol bizim en masrafsız yolumuz oluyor ve problem çözülüyor. Şimdi bu işlemin doğruluğunu kanıtlayalım: Farz edelim G çizgesi bir Hamiltonian Döngüsü barındırıyor. Bu döngünün tüm yolları G çizgesinin yol kümesinin içinde var ve G’ çizgesinde bu yollara karşılık olarak maliyeti 0 olan yollar bulunuyor. O zaman ilk çizgemizdeki yol, G’ çizgesinde de maliyeti 0 olan, en hesaplı Hamiltonian yoluna karşılık geliyor. Aynı şekilde, G’ 0 maliyetli ve istenen özellikte bir yol bulunabilirse, bu yol üzerindeki tüm yollar da 0 maliyetli olmak zorunda. 0 maliyetli yolların G deki karşılığı bir Hamiltonian döngüsünün varlığına karşılık gelmek zorunda çünkü bu yol tüm düğümleri kapsıyor ve hapsinden sadece 1 kez geçiyor. Dışarıda kalan durum bulunmadığından indirgeme işlemi bitmiş oluyor.
- Yapılan işlemler polinomsal zamanda biter.
G’ çizgesini oluşturmak için olabilecek tüm yollardan sadece 1 kere geçiliyor O(V<sup>2</sup>). Yani polinomsal zamanda tüm bu işlemler tamamlanabilir.
Görüldüğü gibi bu büyük ve çözümsüz problemler bir NPC problemin çözümüyle halledilebilecek durumdadır. P=NP? Sorunu yıllardan beri en önemli problem olarak bilgisayar bilimcilerinin aklını kurcalamaktadır ve verilecek olan ödüle rampan hala çözümü bulunamamaktadır. 2002 yılında yapılan bir ankette 100 araştırmacının 61’i “P=NP?” sorusuna hayır cevabını verirken 9’u evet, 22 si kararsız, 8’i ise cevap ne olursa olsun ispatlanmasının imkânsız olduğu cevabını vermiştir. Peki ya sizce NP sınıfı P sınıfına eşit midir? :)
Kaynakça
- http://en.wikipedia.org/wiki/Computation_theory
- http://en.wikipedia.org/wiki/Computational_complexity_theory
- http://en.wikipedia.org/wiki/P_(complexity)
- http://en.wikipedia.org/wiki/Complexity
- http://en.wikipedia.org/wiki/Complexity_classes_P_and_NP
- http://en.wikipedia.org/wiki/NP_(complexity)
- http://en.wikipedia.org/wiki/P_%3D_NP_problem
- http://en.wikipedia.org/wiki/Travelling_salesman_problem
- Introduction To Algorithms 2nd edition Thomas H. Cormen