Merhaba sevgili e-bergi okuyucuları, sizlere bu yazımda, son yazımda olduğu gibi, veriyi etkili ve hızlı bir biçimde kontrol etmek için (ona erişmek; onu değiştirmek, eklemek, silmek) kullanılan yöntemlerden birini anlatacağım: hash tabloları. Hash tabloları, verilerin tek tek ele alınması söz konusu olduğunda hesaplama karmaşıklığı en düşük olan veri kontrol şeklidir; yani mümkün olan en hızlı çözümleri sağlamaktadır.

Hash tablolarının ne zaman avantajlı ve ne zaman dezavantajlı olduğu sebepleriyle beraber daha rahat anlaşılabileceğinden öncelikle hash tablolarının yapısından ve hash fonksiyonlarından bahsetmek istiyorum. Hash tablosu, verilerin kümelenmiş halde tutulduğu bir dizindir. Aslında kümelenmiş kelimesini kullanırken iki boyutlu bir dizin halinde tutulduğunu düşünebilirsiniz; ancak bu her zaman şart değildir. Zaten dizinin ikinci boyuttaki uzunluğunu bir birim alırsanız, aslında tek boyutlu bir dizinden bahsediyor oluruz. Konumuza dönersek, hash tablosunu; yani bu dizini diğerlerinden ayıran özellikler, farklar nelerdir? Tablo büyüklüğü M olan bir hash tablosunun her bir elemanına 0'dan M-1'e kadar indis numaraları verilmiştir ve bu numaralar onların aynı zamanda adresleridir. İndis numarasının aynı zamanda adres olması çok önemli bir noktadır; çünkü dizinlerde herhangi iki elemana ulaşmanın hızı eşittir. Yani bir verinin başta veya sonda olması ona erişme hızınızı hiçbir şekilde etkilememektedir ve bu hızın sabit bir hesaplamasal karmaşıklığı vardır. Daha matematiksel bir ifadeyle karmaşıklığı O(1)'dir. Bunun anlamı da bizim bir elemana ulaşmak için harcadığımız zamanın, verinin büyüklüğüne göre değişmediğidir. Her bir elemana erişim bilgisayarın hafızasındaki herhangi bir noktaya erişmek kadar hızlıdır, ki bu hız hafızadaki bir veri için maksimum hız oluyor. Hash tablolarının da birer dizin olması dolayısıyla aynı hızlar tabii ki onlar için de geçerlidir. O zaman bilmemiz gereken önemli tek bilgi verinin hangi adreste saklı olduğudur. Bunu bildikten sonra istediğimiz veriye çok yüksek hızlarda ulaşmamız mümkün gibi gözüküyor! Mümkün gibi gözüküyor diyorum; çünkü hash tablolarının tam anlamıyla işe yaramadığı bazı noktalar söz konusu. Yine de bu dezavantajından önce hash fonksiyonlarını ve veri adreslerinin nasıl bulunduğunu anlatmak istiyorum. Tahmin etmişsinizdir ki bu fonksiyonlarla adreslerin direk alakası var. Hash fonksiyonlarının kullanıldığı nokta tam olarak bu: adresleri hesaplama ya da -sonuçta bir tablodan bahsettiğimize göre- indis numaralarını hesaplama. Geçen yazımda da bahsettiğim şekilde her bir verinin anahtar bir alanı var; yani sadece o veriye özel olan, bir başka veride aynısı bulunmayan bir bilgiye sahip olmalı. Şimdi hash fonksiyonları için daha matematiksel bir tanım yapabiliriz. Hash fonksiyonları, verilerin anahtarlarından çıkan, indis değerlerini dönen ve anahtar değerlerinin bir sınırının olmamasına karşın indis değerleri belli bir aralıkta olduğu için çoğu zaman birebir olmayan; fakat örten olması beklenen fonksiyonlardır. Çoğu zaman dememin sebebi aslında bu özelliklere uymayan fonksiyonların (yani birebir olan ve örten olmayan fonksiyonlar) hiç değilse teoride yazılabilecek olması; ancak bu fonksiyonlar ya hafızayı çok savurgan bir şekilde kullanacaktır (yersel karmaşıklığı çok yüksek olacaktır) ya da hem yersel hem de zamansal (hesaplama) karmaşıklığı yüksek olacaktır. Bu iki durumdan da kaçınmak isteriz. Hemen yeri gelmişken söyleyelim: hash tablolarının zamansal karmaşıklığı diğer birçok yöntemden az olduğu halde yersel karmaşıklığı çok daha fazladır; bu da doğal olarak hash tablolarını bizim için yerden ziyade hızın önemli olduğu durumlarda kullanmamız gerektiğini göstermektedir. Zaten genelde bu ikisi birbirlerinin karşılığı olarak ödenmesi gereken bir bedeldir; yani zamanda veya yerde verimli bir kullanım için birinden taviz verip diğerindeki verimi artırırız.

Artık hash fonksiyonları konusunu biraz daha genişletebiliriz. Öncelikle birebirlik ve örtenliğin bu konu için özel olarak ne anlama sahip olduğunu açıklığa kavuşturalım. Birebir olması, her bir anahtar için (o anahtara özel) tek bir indis değerinin olmasıdır; yani herhangi iki farklı anahtar değeri için fonksiyonun döndüğü değerler daima farklıdır. Hash fonksiyonlarının birebir olmamasının sebebi şudur; anahtar değerlerinin belli bir aralığı olmak zorunda olmadığı için birebir bir hash fonksiyonunu yaratmak için belirsiz büyüklükte hash tabloları kullanmak gerekir. Bu da teoride sonsuz bir büyüklük oluyor. Bu durumun pratikteki karşılığını düşünecek olursak da anahtar değerlerini sınırlı olduğunu, ancak çok büyük sınırlara sahip olduğunu düşünebiliriz. Bunun sonucunda yine çok büyük hash tabloları yaratmak gerekir; bu da hafızadan çok fazla yer almamız anlamına gelir. Buna ek olarak bir hash tablosunun doluluğunu yansıtan ve “doluluk çarpanı” denilen bir değeri vardır. Birebir olan bir hash fonksiyonuna sahip bir hash tablosunda bu değer sıfıra çok yakın olacaktır. Bu, hafızadan hiç kullanılmadığı halde (çarpıcı bir örnek olsun diye söylüyorum) gerekenden en az on kat daha fazla yer alacak olmamız anlamına geliyor. Ancak dediğim gibi birebir olan bir hash fonksiyonu yalnızca teorik olarak mümkün olduğundan onun üzerine düşünmeye çok fazla gerek yok. Şimdi bir hash fonksiyonunun örten olmasının ne demek olduğundan ve örten olmamasının ne gibi zararları olduğundan bahsedelim. Örten bir hash fonksiyonuna sahip bir hash tablosundaki her bir indis değeri için o indise giden en az bir tane anahtar değeri vardır. Peki, örten olmayan bir hash fonksiyonu kullanılıyorsa bu ne anlama gelmektedir ve bunun ne gibi dezavantajları vardır? Eğer hash fonksiyonu örten değilse tüm indis değerleri için bir tane anahtar bulamayabiliriz. Bu da demek oluyor ki bazı adreslerde asla veri tutulmayacak. Bu durum, tıpkı az önce bahsettiğimiz gibi, gereksiz yer kullanımına sebep oluyor; fakat bu durum sadece yersel değil, dolaylı yoldan da olsa, zamansal karmaşıklığı da artırmaktadır. Eğer tabloda doldurulamayacak adresler varsa (bazı kısımlar her zaman boş kalacaksa) o zaman potansiyel olarak orayı doldurması gereken veriler başka adreslere yerleştirilecektir. Bu yüzden tabloda bazı noktalarda kayıt sayısı artıp taşmalar meydana getirecektir. Bunların olmaması için güzel bir hash fonksiyonundan beklenen, örten olmasının yanı sıra, anahtarları indislere olabildiğince eşit paylaştırmasıdır. Tabii, alacağımız veriyi önceden bilemediğimiz için hash fonksiyonları her zaman eşit paylaştırmazlar ve genelde bazı adreslerde birden fazla kayıt tutmak gerekir. Bu durumlara “çarpışma” denir.

Hash fonksiyonları birebir olmadığı için bazı adres değerlerine birden fazla anahtar değer bağlanır. Bu durumu kontrol etmek için çeşitli yöntemler geliştirilmiştir. Bu yöntemlerin ilki ayrık zincirleme yöntemidir. Bu yöntemde tabloda tutulan bilgiler verilerin kendileri değil; ama işaretleyicileridir. Bu işaretleyiciler verinin kendisini değil de aynı indise giden tüm verilerin oluşturduğu bir listeyi gösterirler. Böylelikle ne kadar çok veri olursa olsun ayrık zincirleme yöntemiyle hepsi tek tabloya sığabilir. Ancak bu yöntemin dezavantajı, çok fazla veri varsa ve listelerdeki eleman sayıları çok yükselirse, listedeki eleman sayısı kadar arama yapmak gerekebilir. Bu durumda hash tabloları en önemli yararı olan tek ya da birkaç aramada veriye ulaşma özelliğini zamanla yitirebilir. Bu nedenle bu yöntem her zaman tercih edilemez.

İkinci önemli yöntem ise açık adresleme yöntemidir. Bu yöntemin kendi içinde çeşitleri vardır. Bunlar doğrusal araştıran, ikinci dereceden araştıran ve çift hash fonksiyonu kullanan yöntemlerdir. Doğrusal araştıran yöntemde temel algoritma şudur: eğer bir adres doluysa veya aradığın kayıt orada değilse ondan bir sonraki adrese bak. Bu kendini tekrar ederek gidebilir; yani bir veri ekleyeceğimiz zaman hash fonksiyonunun döndüğü değerdeki adres doluysa ondan sonraki ilk boş adresi bulana kadar arar ve bulunca veri oraya eklenir. Bu yöntemin de tabii ki bazı dezavantajları var. Eğer tablonun bir kısmında yoğunluk olursa orada uzun, listeye benzer yapılar oluşur. Bu durum kendini daha kötü yönde etkiler; çünkü bu, listenin uzama ihtimalini artırır ve bu şekilde tabloda büyükçe bir ada oluşabilir. Bu adaya birincil kümelenme denir. Genelde de bu adada sadece çok az veri kendi olması gerektiği yerde durur; bu yüzden her operasyonda gereksiz birçok arama yapmak zorunda kalırız. Bunu engellemek için ya doluluk çarpanını (bu sayı sahip olduğun veri sayısının tablonun büyüklüğüne bölümüdür) %50'nin altında tutmak gerekir -ki aslında bu çoğu zaman bizim kontrolümüz altında olan bir sayı değildir- ya da diğer açık adresleme yöntemlerini kullanmak gerekir. İkinci dereceden araştıran açık adresleme aslında mantık olarak doğrusal ile aynıdır. Doğrusalda birinci aramamızı doğru adresten bir sonraki adrese bakarak yapıyorduk, ikinci aramamızı iki sonraki adrese bakarak, n'inci aramamızı da n sonraki adrese bakarak yapıyoruz. İkinci dereceden olunca tahmin ettiğiniz üzere ilk aramada bir sonraki adrese bakarken ikinci aramada -ikinin karesi olan- dört sonraki adrese bakarak ve n'inci aramamızı da n2 sonrasındaki adrese bakarak yapıyoruz. Bu yöntemde birincil kümelenme oluşmaz; ancak aynı yere gitmesi gereken veriler tekrar bir ada yapısı meydana getirebilir (her ne kadar bitişik olmasalar da ada denir). Bu adalara da ikincil kümelenme denir. Bu yöntemin sağlıklı çalışması için tablo büyüklüğünün bir asal sayı olması çok önemlidir; aksi halde bazı durumlarda tabloda asla boş yer bulunamayabilir.

Çift hash yöntem, aslında önceki yöntemin özel bir durumu oluyor; ama bu sefer adrese eklenen değeri iki kez kendiyle çarpmak yerine bu değer başka bir hash fonksiyonuyla çarpılır. Buradaki avantajlar ve dezavantajlar tamamen bu fonksiyona bağlı olduğu için önceden bir yorum yapmak yanlış olur; ancak yine de davranış olarak ikinci dereceden araştıran yöntemle benzerlik gösterdiği biliniyor.

Şu ana kadar bahsettiğim yöntemlerin tamamı durağan hash'leme adı altında geçer. Durağan hash'lerde tablo büyüklüğü değişiklik göstermez; hep sabittir. Durağan hash'e ek olarak doğrusal hash'leme ve genişleyebilen hash'leme de vardır. Her iki yöntemde de tablo boyutunda değişikliğe gidilir. Yalnız bu yöntemleri kullanırken anahtarın sayısal bir değer olarak seçilmesi gerekir. En azından, önce o anahtar değerine sayısal bir karşılık verilmelidir. Daha sonra bu sayının ikili sistemdeki karşılığına göre adresleme yapılır. Doğrusal hash'lemeyle ilgili olarak ayrık zincirleme yapısının var olduğunu söylemeliyiz; ancak sadece bununla kalınmamış, onun üzerine yeni yöntemler de eklenmiştir. Doğrusal hash'lemede anahtarın sondan belli bir sayıdaki (bu sayı k olsun) rakamına bakılır (tabii ikili sistemde baktığımız için sondan k bitine bakılır da diyebiliriz). “k” adet bite karşılık gelen 2k tane adres seçilebilir; yani tablo büyüklüğü başlangıçta 2k'dır. Daha sonra doluluk çarpanı tercihen yaklaşık %70'e gelince tablonun en sonuna yeni bir boşluk eklenir. Başlangıçta tablonun ilk indisi tabii ki 0 ve son indisi 2k-1 iken bu yeni eleman ile son indis değeri 2k olur. Tekrar yeni eleman eklenirse 2k+1 olur ve bu şekilde tablo genişler. Tabii ki sadece sondaki k bite bakılarak bu yeni adreslere ulaşılamaz. O yüzden artık hash fonksiyonumuzu da değiştirmemiz gerekmektedir. Dikkat edilecek olursa ilk eklenen yeni adres değeri olan 2k'nın son k biti sıfırlarla doludur ve sadece k+1'inci biti birdir. Benzer şekilde 2k+1'in ilk biti bir, sonuncuya kadar olanlar sıfır ve son biti yine birdir; yani yeni eklenen adres değerlerinin tablonun başlangıcındaki adres değerlerinden tek farkı, yeni kullanılmaya başlanan k+1'inci bittedir. O halde biz, sırada hangi adresteki listeyi iki tane listeye dönüştüreceğimizi hafızada tutar (tutulan bu sayıya sınır değeri denir) ve ondan öncekiler için son k+1 bite, sonrakiler için ise son k bite bakarak tablodaki yerlerini bulabiliriz. Artık yeni hash fonksiyonumuz da hazır olduğuna göre doğrusal hash'lemeyle ilgili olarak bilinmesi gereken son noktayı da söyleyebiliriz: sınır değerimiz her arttığında önceden eklenmiş verilerden yeni eklenen listeye gitmesi gerekenler gönderilir ve bu sayede dağıtım biraz dengeli hale getirilmiş olur.

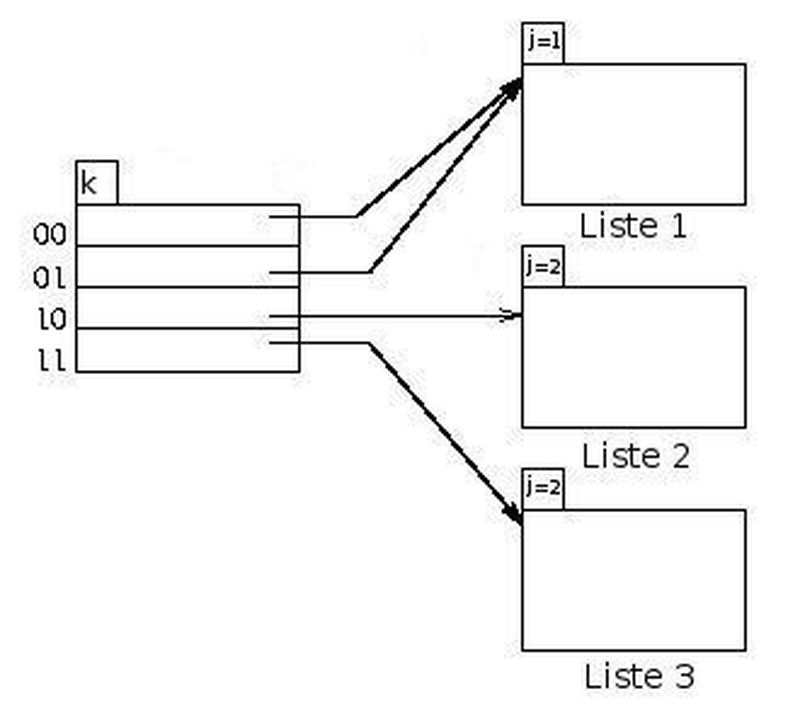
Genişleyebilen hash'leme mantık olarak doğrusal hash'lemeyle çok büyük benzerlik gösterse de yapısı biraz farklıdır. En önemli farkı, genişleyebilen hash'lemede listelerin boyutu sabittir; yani eğer iki boyutlu dizin tanımını hatırlayacak olursak ikinci boyutta bir büyüme gözlenmez. Buna karşın, birinci boyutta -yani direk olarak tablo büyüklüğü denilen sayıda- bir büyüme olur. Benzerliklerine gelecek olursak, aynı doğrusalda olduğu gibi anahtar değerinin k bitine bakılır; ancak bu sefer son k bitine değil ilk k bitine bakılır. Bir büyüme koşulu vardır; yalnız bu sefer büyüme koşulu, doluluk çarpanının belli bir değere ulaşması değil de hash tablosunun herhangi bir indisinde tutulan bir listenin dolmasıdır. Liste dolduğunda tüm tablonun büyüklüğü iki katına çıkar. Bu büyümeyle artık ilk k+1 bite bakıldığı için büyüklük iki katına çıkmış olur. Aslında var olan liste sayısı yine bir artar. Yeni adres değerleri eğer büyüme olmadıysa eskiden tuttuğu yeri göstermeye devam eder; fakat büyüme gerçekleşirse yeni oluşan listeyi göstermeye başlar. Burası biraz karışık gibi durabilir; o yüzden daha iyi açıklamam gerektiğini düşünüyorum. Tekrar doğrusal hash'lemeyi düşünecek olursak, orada tablonun boyutu birer birer artıyordu ve sadece sınırdan öncekiler için k+1 bite bakılıyordu. Bunu şu şekilde de yorumlayabiliriz: aslında diğerleri için de k+1 bite bakılıyor; ancak sadece k+1'inci biti fark ediyorsa iki adres değeri aynı listeyi işaretliyor. Aynı mantıkla genişleyebilen hash'lemede de büyümenin ardından k+1 bite bakılır; ancak bazı adresler (büyütmeye ihtiyaç duyulmayanlar) aynı listeleri göstermeye (önceki k bite bakılırken nereyi gösteriyorlarsa) devam ederler. Genişleyebilen hash'lemede bunlara ek olarak, bu yapıyı kolaylaştırmak adına her listenin ayrıca tuttuğu bir j değeri vardır. İşte tam olarak az önce bahsettiğimiz durumlarda o k+1 bitin sondan kaç tane biti gereksiz bu sayıyı tutuyor. Büyüme olduğu halde aynı yeri göstereceklerse bu j değeri de bir artar. Bu sayede yine aynı bitleri kontrol etmiş oluruz. Tabii ki, söylemedim ama, aynen doğrusal hash'leme de olduğu gibi genişleyebilende de büyümenin ardından dolan listedeki elemanların tekrar dağıtımı yapılır. Yeni açılan listeye gitmesi gerekenler öncekinden silinir ve yeni listeye taşınır.

Hash tablolarının hız konusunda çok başarılı olması gibi birçok iyi yanı olmasın karşın, hatırlatmakta ve dikkat etmekte fayda var: sadece eleman tabanlı yaklaşımda hash tablolarının gücünü görebiliriz. Eğer aradığımız bilgi tek bir elemana değil de belli bir aralığa yönelikse hash tabloları aynı kullanışlılığa sahip değildir. Örneğin anahtar değerleri 200 ile 300 arasında olan kayıtları bulmak istediğimizde 200 ile 300 arasındaki her bir değer için ayrı bir arama yapmamız gerekecektir. Bu da çok verimsiz bir arama yöntemi olacaktır; o yüzden hash tablolarını kayıt tabanlı veri kontrolü için kullanmak gerekir.

Sonuç olarak eleman tabanlı veri kontrol sistemlerinde mümkün olan en hızlı yöntemlerden biri hash tablosu kullanmaktır; fakat kazanacağınız hız karşılığında yerden kaybedeceğinizi ve aralık araması gibi birkaç yeteneğinizden mahrum kalacağınızı unutmayın.

Bir dahaki sayımızda görüşmek üzere, kendinize iyi bakın.