Merhaba değerli e-bergi okuyucuları,
Bu yazıda sizlere geri iz sürme (backtracking) algoritmalarından bahsedeceğim. Geri iz sürme mantığı çok çeşitli problemlerin çözümünde kullanılabilecek, bir veya tüm çözümleri bulmamıza imkan tanıyan genel bir algoritmadır. Sonlu bir problemin, sonlu zamanda tüm çözümlerinin bulunmasını garantiler. "Geri iz sürme"yi; çözmek istediğimiz problemin olası çözümleri arasından doğru olanı deneme-yanılma ile bulmaya çalışmak, bir başka deyişle, sonuca ulaşana kadar seçimleri değerlendirmek olarak ifade edebiliriz.
“Backtrack” teriminin 50’lerde Amerikan matematikçi Lehmer tarafından kullanıldığını ve yerleşik olarak geri iz sürme yeteneği barındıran ilk dilin SNOBOL olduğunu söyleyebiliriz. Ayrıca, geri iz sürme tekniği; mantık programlama dillerinin (Logic Programming Languages) temelini oluşturur.
Geri iz sürme algoritmasını, yalnızca olası ve kısmi bir çözüm önerebildiğimiz ve bu çözümün gerçek bir çözüme tamamlanıp tamamlanamayacağını zorlanmadan anlayabildiğimiz problemlerde kullanabiliriz. Geri iz sürme; tüm ihtimalleri değerlendiren brute-force’dan genelde çok daha hızlı çalışır, çünkü, yanlış ihtimallerin büyük bir kısmını değerlendirmeden devam eder. Bu bağlamda, geri iz sürmeyi brute-force’un sistemli hale getirilerek iyileştirilmiş bir türevi olarak düşünebiliriz.
Geri iz sürmeile bir problemi çözerken, devamlı olarak olası çözümler geliştiririz. Bunlar kabullere dayanan geçici çözümlerdir ve yanlışlığı anlaşıldığı anda (problemin sınırlarına bağlı kalarak çözümün devam ettirilememesi durumu) bu çözümü terkederek son varsayımı yaptığımız noktaya döner ve varsayımımızın yanlış olduğu bilinciyle diğer ihtimal veya ihtimalleri değerlendiririz.
Buraya kadarki kısmı bilinir bir örnekle somutlaştırayım:
Sudoku geri iz sürme kullanarak çözülebilecek problemlerdendir. Hemen herkes tarafından bilinir olsa da kısaca açıklamakta fayda olabilir: Sudoku, 9 x 9 boyutunda bir oyun tahtasına her yatay ve dikey sıraya 1'den 9'a kadar sayıları sıralamaya ve her 3 x 3' lük küçük karelerde de tekrar etmeyecek şekilde rakamları yerleştirmeye dayanan bir oyundur. Bulmacanın kendisinde bazı rakamlar yerleştirilmiştir ve kalanları doldurmamız beklenir. Sayıları aynı yatay ve dikey hizada tekrar etmeyecek şekilde yerleştirmeye başlarız ve bu şekilde devam edemediğimiz bir noktaya gelirsek yerleştirdiğimiz bazı sayıları değiştirerek çözüme gitmeye çalışırız. Eğer bunu sistemli bir şekilde yapıyorsak, mutlaka sonuca ulaşırız ve burada yaptığımız şey aslında geri iz sürme algoritmasını kullanmaktır.
Şimdi geri iz sürme kullanarak 4 x 4’lük bir sudokuyu çözelim:
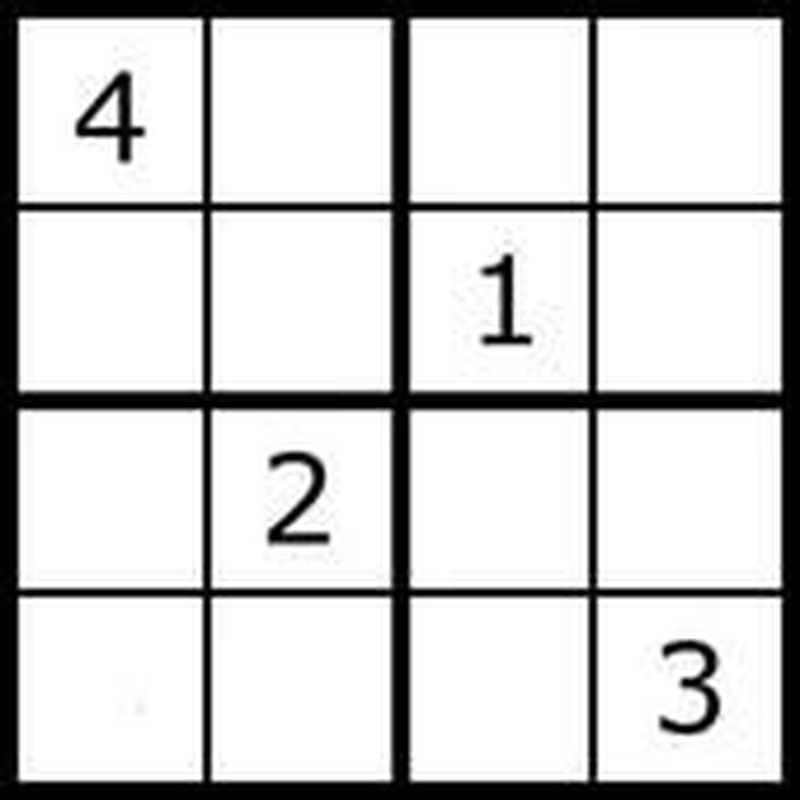
Başlangıçta problemimiz yandaki gibi olsun. Kısaca kullanacağımız tekniği özetlemek gerekirse; sol üst köşeden başlayarak kareleri 1’den 4’e kadar sayılarla dolduracağız. İlk olarak 1 yerleştirmeye çalışacağız ve gözetmemiz gereken 3 kuralı ihlal ediyorsak 2 yerleştirmeyi deneyeceğiz.
Bu 3 kural:
- Dikey sırada sayı tekrarı olmaması
- Yatay sırada sayı tekrarı olmaması
- 2 x 2’lik küçük karelerde sayı tekrarı olmaması
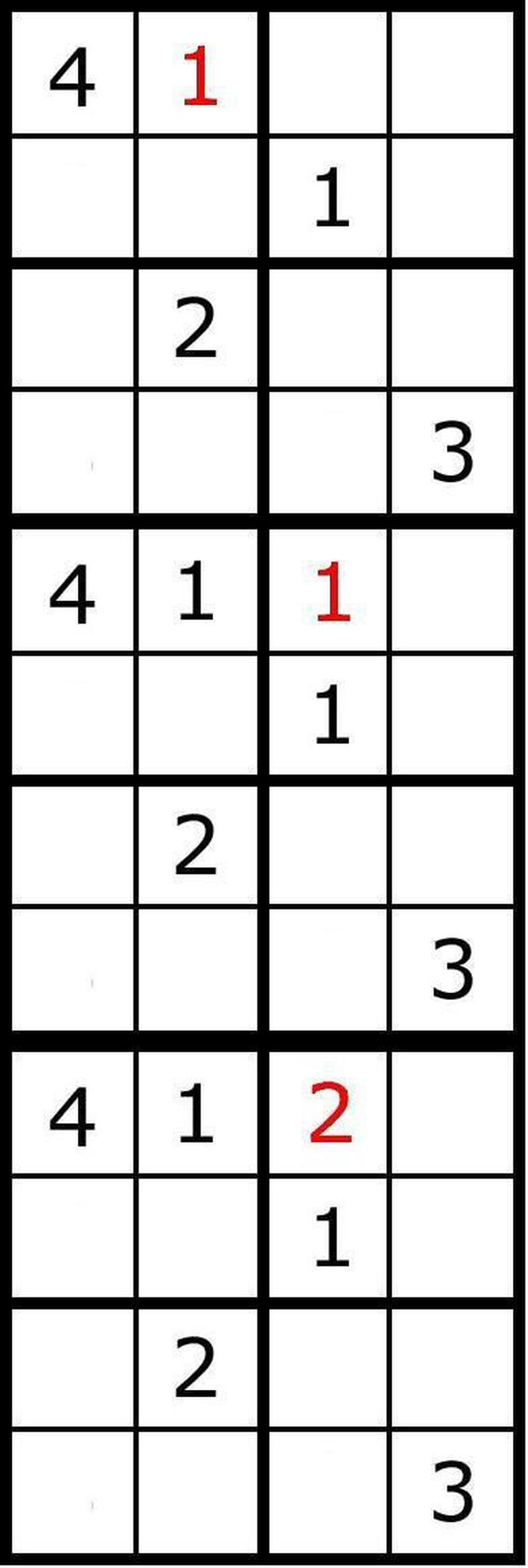
Boş ilk kareye 1 yerleştirerek başlıyoruz.
Oyun kurallarını ihlal eden bir durum olmadığı için diğer kareye 1 yerleştirerek devam edebiliriz.
Böylece 3 kuralı da ihlal etmiş olduk. Bu noktada geri dönmeli ve kareye 1 yerleştirilmesi gerektiği varsayımımızı değiştirmeliyiz. 2 yerleştirmeyi deneyeceğiz.
Mükemmel.
Üst satırdaki son kareyi doldurmaya çalıştığımızda hiçbir sayının şartları sağlamadığını görüyoruz. Bu durumda son varsayımımızın (3. karede 2 olması gerektiği) yanlış olduğunu anlıyoruz ve bu kareye 3 yerleştirerek çözümü geliştirmeye devam ediyoruz.
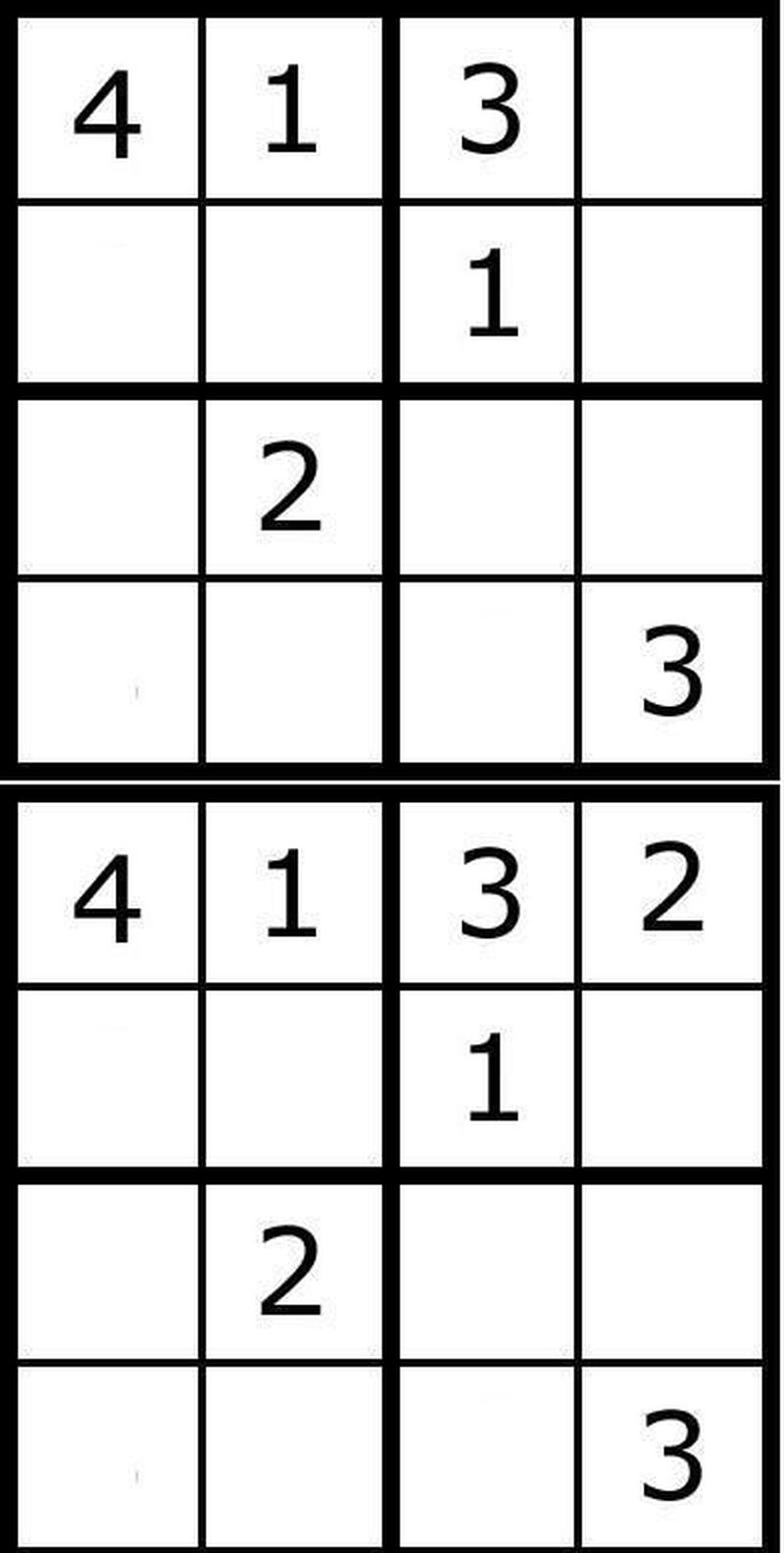
4. kareye her zaman yaptığımız gibi 1 yerleştirerek başlayacağız. Ancak yatay hizada başka bir 1 olduğundan, sayımızı değiştirip 2 yazmayı deneyeceğiz.
Nihayet üst satırı başarıyla tamamladık! Farkettiğiniz gibi geri iz sürme ile çözüme giderken çok sayıda deneme yapmamız gerekiyor.
Bu örnekle geri iz sürmemantığını anlamış olduk.
Bulmacalarda karşımıza çıkan labirentler de geri iz sürme mantığıyla çözülebilecek problemlerden.
Aynı mantıkla; çıkmaz bir yolla karşılaştığımızda, geri dönerek bu noktada daha önce döndüğümüz yolun dışındaki bir seçeneği tercih etmeli ve bu şekilde sonuca ulaşmalıyız. Bu problemde, en kısa yol kavramından da bahsedebiliriz. Çözümlerin tamamını bulup analiz etmeden en kısa yolun hangisi olduğunu bilmek mümkün değildir. Geri iz sürmekullanarak birden fazla çözüm elde edeceksek, probleme bir çözüm bulduğumuzda işlemi sonlandırmadan kaldığımız yerden geri iz sürmeye devam ederiz.
Geri iz sürme genel bir tekniktir ve her uygulaması için özelleştirilmesi gerekir. Geri iz sürme işlemini hangi noktada sonlandıracağımız ise neyi hesaplamaya çalıştığımıza bağlıdır. Tek bir çözüm arıyorsak, her adımda elde edilen çözümün doğruluğunu kontrol edip doğru bir çözüm bulunduğunda aramayı sonlandırabiliriz. Ancak kimi durumlarda tüm çözümleri bulmamız gerekebilir(en kısa yol). Şimdi geri iz sürme kullanarak çözebileceğimiz diğer bilindik problemlere ve bunu nasıl yapacağımıza bakalım:
Permütasyon Oluşturma Problemi
Verilmiş bir kümedeki elemanlardan olası tüm permütasyonları yaratmak için geri iz sürme kullanılabilir. Tekrar eden elemanlardan kaçınmak için, permütasyonun i. elemanının kendisinden önceki tüm elemanlardan farklı olmasına dikkat etmek gerekir.
Örnek olarak a, b, c, d harflerini düşünelim. Bu elemanlarla oluşturabilecek permütasyon sayısı 4! = 24’tür. abcd ile başlayıp dcba ile biten bu permütasyonları oluştururken nasıl bir mantık izlendiğini kısaca izah etmeliyiz. a karakteriyle başlayıp devam ederek ilk permütasyon olan abcd’ye ulaşırız. İkinci permütasyonu elde ederken son karakter d olamayacağından bir önceki karakterin c olmaması gerektiğini anlarız. Bu karakteri sonraki eleman d ile değiştirdiğimizde abdc permütasyonuna ulaşırız. Bu mantıkla devam ederek tüm permütasyonları elde ederiz. Aşağıdaki C++ uygulamasını inceleyebilirsiniz.
#include < iostream >
using namespace std;
void swap (char *x, char *y)
{
char t;
t = *x;
*x = *y;
*y = t;
}
void permutation(char *str, int i, int k)
{
int j;
if (i == k) cout << str << endl;
else
{
for (j = i; j <= k; j++)
{
swap((str + i), (str + j));
permutation(str, i + 1, k);
swap((str + i), (str + j)); // Geri iz sürme
}
}
}
int main()
{
char string[] = "abcd";
permutation(string, 0, 3);
return 0;
}Vezir Bulmacası (The Queens Problem)
Bu problemde, n x n’lik bir satranç tahtası üzerine n adet veziri, birbirlerini tehdit etmeyecek şekilde yerleştirmek gereklidir. Bir vezir yatay, dikey ve çapraz doğrultularda hareket edebilir.
İlk veziri tahtanın sol alt köşesine yerleştirdiğinizi hayal edin. İkinci vezir, ilk vezirin olduğu yatay, dikey ve çapraz hizalarda bulunamaz. Bu teknikle olasılıkların büyük bir kısmını test etme zorunluluğundan kurtulduğumuzu söyleyebiliriz. Devam ettiğimizde n adet veziri yerleştiremiyorsak, son yerleştirilen vezir için bir sonraki olası konumu deneyerek devam ederiz.

8 vezir probleminin çözümlerinden biri
Bu yazıda geri iz sürme algoritmasının ne olduğuna, çalışma mantığına ve çözümünde kullanılabileceği bazı problemlere değindik. Brute-force’dan pek de karmaşık olmayan, ancak çok daha verimli olan bu teknikle yazıda bahsedilmeyen daha pek çok problem çözülebilir.
KAYNAKLAR: