Merhaba arkadaşlar bu ay sizlere little endian – big endian hakkında bir yazı hazırladım, umarım beğenirsiniz. Bu terimlerin nereden geldiğini öğrenerek başlayalım yazımıza. Jonathan Swift tarafından 18. yüzyılda yazılan Gülliver’in Maceraları adlı kitaptan gelmektedir bu terimler. İki çatışan grup az pişmiş yumurtanın açılıp açılmaması konusunda bir anlaşmaya varamamıştır. Bu durum da küçük son ve büyük son terimlerine karşılık gelmektedir. Şimdi gelelim yazımızın detaylarına.
İnsanların soldan sağa veya sağdan sola alfabelere sahip olmaları gibi işlemciler de baytları saklarken önemli baytın solda veya sağda olmasına göre sınıflandırılır. Buna sıralılık veya bitimlilik (endianness) da denir. Diğer bir deyişle endianness bayt sıralamasıdır. Kıymetli baytın solda olduğu sıralamaya big-endian (düz sıralı), en sağda olduğu sıralamaya da little-endian (ters sıralı) denir. Bu kavramları tam olarak anlamak için öncelikle hızlı bir şekilde hafızayı inceleyelim.
Hafızayı en basit ve kaba şekliyle baytların saklandığı uzun bir dizin şeklinde ifade edebiliriz. Normalde dizindeki herhangi bir yeri ifade etmek için “indis” terimi kullanılırken, bilgisayar bilimcileri hafızadan bahsederken “adres” terimini daha çok kullanılırlar. Her bir adres hafıza dizininin bir elemanını tutar. Bu eleman genelde bir bayt olur ama bu bir zorunluluk değildir. Diyelim ki bir kutucuk (word) 32 bit yani 4 bayt olsun. Tam sayılar, tek duyarlı ondalık sayılar, hepsi 32 bit uzunluğunda yani bir kutu uzunluğundadır. Peki biz bunları hafızayı nasıl koyacağız? Sonuçta her bir hafıza adresi tek bir bayt depolayabilir. Sorumuzun cevabı basit: 32 bit uzunluğundaki sayımızı 4 bayta bölücez. Mesela sayımız 16 tabanında şu şekilde ifade edilsin 12CD34AB16 .16 tabanında her basamak 4 bit ile ifade edildiğinden sayımızı ifade edebilmek için 8 tane 16 tabanında basamağa ihtiyacımız olacaktır. Böylece sayımızı şu şekilde ayırabiliriz: 12 CD 34 AB. Ayrılmış bölümlerin her biri birer bayt oldu böylece. Şimdi gelelim sayımızı hafızada depolamaya. Bunun iki yöntemi vardır.
1)Büyük Endian
Bu yöntemde önemli bayt en küçük adreste depolanır. Bu durumda sayımız tablodaki gibi olur.
Görüldüğü gibi önemli bayt olan 12 değeri en küçük adreste depolandı. Sonraki bayt -CD- bir sonraki adreste ve buna benzer şekilde devam ederek sıralanırlar. Bu 16 tabanında soldan sağa okuma sırasına çok benzer. Bir diğer örneğimiz 0A0B0C0D olsun. Bunu da bölümledikten sonra (0A 0B 0C 0D) hafızada aşağıdaki durumda depolanır. Motorola işlemciler düz sıralı (Big Endian) bayt sıralamasını kullanırlar. Adobe Photoshop, IMG(GEM Raster), JPEG, MacPaint, SGI, Sun Raster gibi birçok dosya biçimi de bu sıralama yöntemini kullanır.
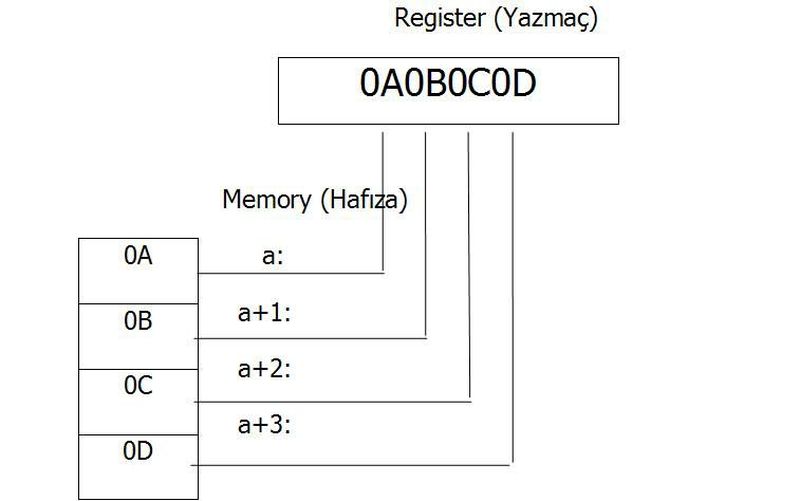
2)Küçük Endian
Bu yöntemde ise tam tersi bir yol izleriz. Aynı şekilde sayımızı bölümleriz. Bu sefer ise önemli bayt en büyük adreste depolanır. İlk sayımızı (12CD34AB) tabloda görelim.
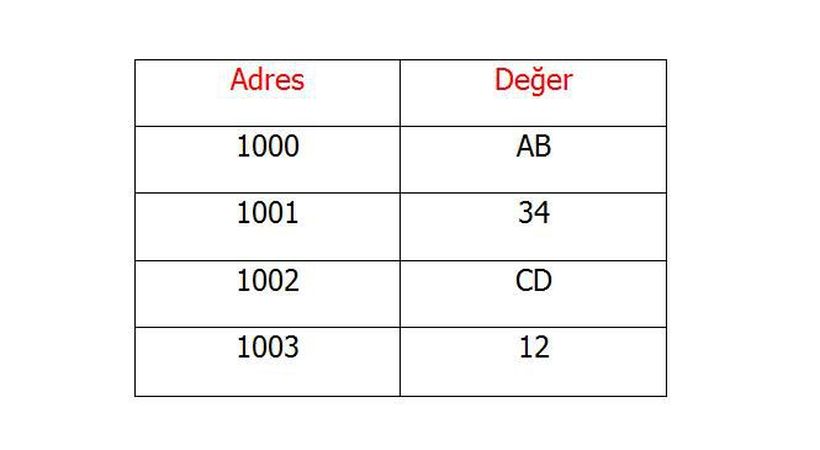
Burada da önemli bayt en büyük adreste sıralandıktan sonra diğer baytlar sırasıyla azalan adreslerde depolanır. Intel işlemciler ters sıralı, yani kıymetlisi sonda (Little Endian) bayt sıralamasını kullanırlar. BMP, GIF, FLI (Autodesk Animator), PCX (PC Paintbrush), QTM (Quicktime Movies, on a Mac!), TGA (Targa) gibi birçok dosya biçimi de bu sıralamayı kullanır.
Hangi yöntem daha kullanışlı ve daha iyi?
Bu iki yöntem üzerinde birçok tartışma vardır. Bu tartışmalar daha çok PC ve Mac arasındadır. Tabi ki iki yöntemin de kendi avantaj ve dezavantajları vardır. Ters sıralama yönteminde, çevirici dil komutları 1,2,4 veya daha uzun bayt sayısını almak için bütün formatlarda aynı yöntemi kullanır, ki şu şekilde gerçekleşir: İlk olarak 0. konumdaki en düşük bayt alınır. Ayrıca adres konumu ve bayt sırası arasında birebir ilişki olduğundan çoklu duyarlı matematiksel ifadeleri yazmak daha kolay olmaktadır bu yöntem ile. Düz sıralama yönteminde ise önemli bayt ilk olarak geldiği için daima bir sayının pozitif mi negatif mi olduğunu 0.konumdaki bayta bakarak anlayabiliriz. Sayının ne kadar uzun olduğunu anlamak veya sayının pozitif mi negatif mi olduğunu belirleyen baytı bulmak için diğer baytları taramamıza gerek yoktur. Sayılar ayrıca yazıldığı gibi hafızada depolanırlar, dolayısıyla ikilik tabandan onluk tabana çevirme işlemleri oldukça verimlidir.
Sıralamadan doğan problemler
Diyelim ki bir dosyaya tam sayı bir değer kaydettiniz ve sonra bu dosyayı sizinkiyle eşleşmeyen bir sıralama kullanan bir makinaya gönderdiniz. Yazdıklarınızı okumak istediğiniz vakit, zıt sıralama olduğundan dolayı ters bir biçimde okursunuz sayınızı ve bu hiç mantıklı değil. Ayrıca sayıları ağ üzerinden gönderirken de bu tarz problemler doğabilir. Bu ilk durumdan daha kötüdür; çünkü gönderdiğiniz verileri alan makinanın hangi sıralamayı kullandığına karar veremezseniz genelde. Bu tarz sorunları engellemek için ‘ağ bayt sıralaması’ (network byte order) kullanarak verileri 4 baytlık gruplar halinde gönderilmesi bir çözüm yoludur. Bu yöntem ters veya düz sıralamalardan birini rastgele seçer, düz veya ters sıralı olma zorunluluğu yoktur. Gönderdiğimiz makina ağ bayt sıralamasıyla aynı sıralama yöntemini kullanıyorsa tamamdır bir değişikliğe gerek yoktur. Fakat durum ters ise o zaman baytları ters çevirmek gerekmektedir.
Evet değerli e-bergi okuyucuları bir yazımızın daha sonuna geldik. Kısa bir yazı oldu ama bir sonraki ay ondalık sayıların hafızada nasıl saklandığını anlatmaya çalışacağım. Bu yazı bir sonraki için giriş niteliğinde olsun istedim. Zamanınızı ayırdığınız için teşekkürler, herkese şimdiden iyi bayramlar dilerim :)