Merhaba sevgili e-bergi okuyucuları, yeni sayımızda sizlerle tekrar beraberiz. Bu yazımda en kısa yol probleminden ve e-bergi’de daha önce biyografisini sunulan Edsger Wybe Dijkstra’nın kendi adıyla da anılan en kısa yol algoritmasından bahsedeceğim.
Öncelikle en kısa yol probleminin ne olduğunu açıklığa kavuşturmak istiyorum. İki nokta arasında ilerlerken her zaman kuş uçuşu gitmek yani doğrusal yol almak mümkün olmayabilir. Bu durumda en kısa yol için alternatiflerimizi düşünmemiz gerekir. En kısa yol problemi, adından kabaca çıkarabileceğimiz gibi iki nokta arasındaki en kısa yolu bulma arayışıyla doğmuştur. Ancak günümüzde bunun biraz ötesine geçmiştir (zaten bu yüzden burada bahsetme ihtiyacı duyuyoruz yoksa seyahat acentesi açacağımız yok) :P. En kısa yola ek olarak en ucuz hat, en hızlı bağlantı, hatta en az hamleyle rubik küp çözmek gibi problemler de yine bu problemin kapsamında kalmaktadır. Peki, bu problemlerin aralarındaki benzerlik neden kaynaklanmaktadır, neden aynı kapsamdalardır? Bu sorunun cevabı aslında biraz çözüm yolunda gizli. Genel olarak algoritmik bir çözümü olan problem iyi tanımlanmış olmalıdır. Yani daha açık bir dille ifade etmek gerekirse problem matematiksel nesneler ile ifade edilebilir olmalıdır. Bu problemlerin matematiksel ifadeleri aynı olduğu için çözümleri de aynı kapsamda yer almaktadırlar.
En kısa yol problemindeki matematiksel nesnelerimiz grafiklerdir. Grafikler, biri noktalar diğeri ise kenarlar kümesi olan ve bazı özellikleri sağlayan iki kümenin birleşimidir. Bu özellikler konumuz için çok önemli olmadığından bunları atlıyorum. Yandaki resime baktığımızda 1, 2, 3, 4, 5 ve 6 noktalarını ve bunları birleştiren doğrular görüyoruz. Zaten grafik olarak bahsettiğim şey, problemlerin çoğunda görsel olarak bu ve bunun benzerleridir. Bu grafiğe en kısa yol probleminin örnek bir grafiği olarak baktığımızda, noktaları şehirler, doğruları da şehirler arası yollar olarak düşünebiliriz. Burada gösterilmeyen önemli bir nokta var ki, o da en kısa yol probleminde kenarların uzaklık, zaman vs. olarak değerleri olmalıdır.Bu değerlere kenar ağırlıkları da denir ve pozitif olmalılardır (bazı durumlarda negatif olabilirler genelde değillerdir aksi takdirde bazen sonsuz kısalıkta yollar bulmayı mümkün kılabilirler yani yolu ne kadar çok gidersen o kadar kısalıyormuş gibi J). Grafikleri kısaca açıkladıktan sonra artık en kısa yol problemlerinde aranan minimizasyonun her zaman iki nokta arası olmayabileceğini de söyleyebilirim. Bazen her bir noktadan her bir noktaya (tüm ikililer) bazen bir noktadan her noktaya, (tek kaynak), bazen de her noktadan bir noktaya (tek hedef) olan en kısa yolu bulmak gerekebilir.
Peki, grafikleri de anladığımıza göre şehirleri en az yol giderek nasıl gezeriz ya da bir bağlantıyı hangi hatları kullandığımızda en hızlı haliyle kullanabiliriz? Çeşitli durumlar için çeşitli algoritmalar mevcut. Bunlardan kısaca bahsettikten sonra asıl bahsetmek istediğim algoritma olan Dijkstra’nın algoritmasını daha detaylı bir şekilde açıklayacağım.
- Bellman-Ford algoritması, tek kaynak problemlerini kenar ağırlıkları negatif olduğu durumlarda da çözer.
- A* arama algoritması, iki nokta arası en kısa yolu aramayı hızlandırmak için sezgisel yöntemler kullanarak çözüme ulaşır.
- Floyd-Warshall algoritması, tüm ikililer probleminin çözümünde kullanılır.
- Johnson’ın algoritması, Floyd-Warshall gibi tüm ikililer problemlerini çözmeye yarar ancak daha yoğun grafiklerde daha hızlı çalışabilir.
- Bozunma teorisi, en kötü ihtimalle yerel en kısa yolları bulur.
Artık Dijkstra’nın algoritmasından bahsedebilirim. Bu algoritmaya neden bu kadar önem verdiğimi merak ediyorsanız; bu algoritmanın en önemli özelliği uygulaması çok basit olduğu halde en başarılı, en verimli algoritmalardan biri olmasıdır. Dijkstra’nın algoritması negatif kenar ağırlığı bulunmayan grafiklerde tek kaynak problemlerini çözmekte kullanılır. Yönlendirmede (routing) sıkça kullanılan bir algoritmadır. Gelelim algoritmanın nasıl çalıştığına. Tek kaynak problemimizdeki kaynak noktamıza başlangıç noktası diyelim. Bir noktanın uzaklığı olarak tanımladığımız değer ise o noktanın başlangıç noktasına olan uzaklığı olsun. Bu algoritmanın 5 adımı vardır ve amaç adım adım noktaların uzaklıklarını azaltmaktır.
- İlk olarak her bir noktaya bir uzaklık değeri vermek gerekir. Başlangıç noktasının uzaklığı 0 olarak ayarlanır ve diğer tüm noktaların başlangıç uzaklığı sonsuz olarak ayarlanır.
- Bütün noktalar ziyaret edilmemiş olarak işaretlenir ve başlangıç noktası aktif nokta olarak seçilir.
- Aktif nokta için, ziyaret edilmemiş bütün komşularının başlangıç noktasından uzaklıkları hesaplanır ve eğer bu değer komşu noktaların o anki uzaklık değerinden küçük ise o noktanın uzaklık değeri yeni bulunan ile değiştirilir.
- Ziyaret edilmemiş bütün komşuları hesapladıktan sonra aktif nokta ziyaret edildi olarak işaretlenir. Ziyaret edilmiş bir noktanın uzaklığı bir daha asla hesaplanmaz; hesaplanılmış değer nihaidir ve minimumdur.
- Ziyaret edilmemiş ve uzaklığı en düşük nokta aktif nokta olarak seçilir ve 3. adımdan devam edilir.
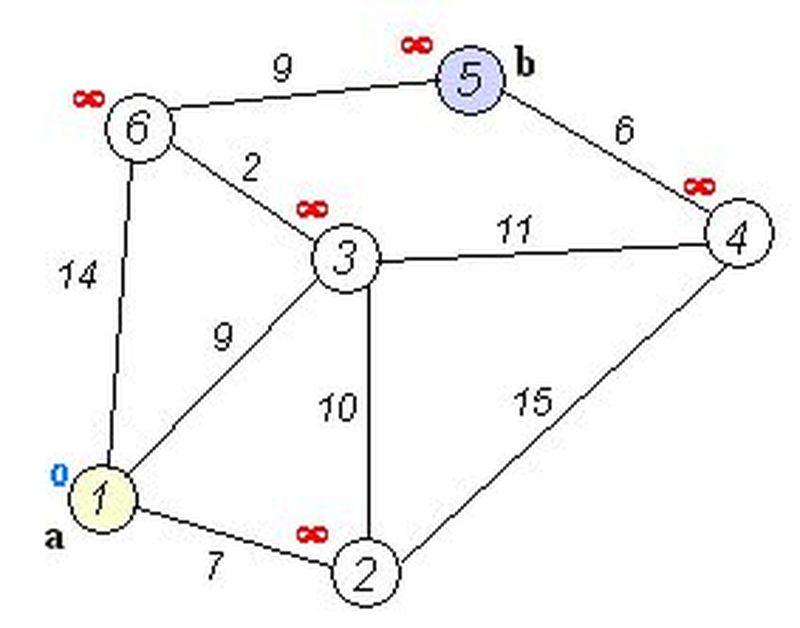
Dijkstra’nın en kısa yol algoritmasını bir örnek üzerinde göstermek daha iyi anlamak için yararlı olacağından hemen bir örneğe başvurmakta fayda görüyorum. Yanda gördüğünüz şekilde “a” noktası başlangıç noktasıdır vebaşlangıçta uzaklığı 0’a eşitlenir. Diğer tüm noktaların uzaklıkları ise sonsuz olarak ayarlıdır. Tüm noktalar ziyaret edilmemiş olarak işaretlenir (bu şekilde beyaz renkli olması anlamına geliyor) ve başlangıç noktası aktif nokta olarak seçilir. Daha sonra aktif noktadan etrafındaki tüm ziyaret edilmemiş komşularına gidilerek uzaklıklar toplanır yani aktif noktanın değeri ile üzerinden geçilecek kenarın ağırlığı toplanır. Şekile göre anlatmam gerekirse başlangıç noktasının üç komşusuna uzaklıkları (0+14, 0+9, 0+7 şeklinde. Bu işlemlerdeki 0’lar aktif noktanın değerinden gelmektedir) toplanarak hesaplanır. Üçünün de başlangıç uzaklık değeri sonsuz olduğundan ve bulunan değerler sonsuzdan küçük olduğundan hepsinin uzaklık değerleri yeni bulunanlar ile değiştirilir. Daha sonra başlangıç noktası ziyaret edildi olarak işaretlenir (bu şekilde kırmızıya boyamak oluyor). Ardından ziyaret edilmemiş noktalardan uzaklık değeri en küçük olan aktif nokta olarak seçilir. Bu durumda uzaklık değeri 7 olan nokta seçilir. Aynı şekilde bu noktadan da tüm ziyaret edilmemiş komşular için uzaklık hesaplanır. Bu noktada farklı olarak 7+10 olarak hesaplanan değer daha önceden bulunmuş değerden (0+9’dan) yüksek olduğu için onun uzaklığını değiştirmez. Daha sonra tüm komşular bitince en küçük uzaklık değerine sahip ziyaret edilmemiş noktanın 3. nokta olduğu gözükür ve bu nokta aktif nokta olarak seçilir. Bu şekilde en son bulunan uzaklık değerlerinden daha küçük uzaklık değerine sahip nokta olmadığında algoritma durur ve en kısa yolun maliyeti hesaplanmış olur.
Aslında kısaca bu algoritmada yapılan iş, sürekli olarak en kısa yoldan ilerleyip bir dahaki noktalar için daha kısa bir yol bulabilir miyiz diye aramak oluyor. Yani temel olarak, sürekli en düşük değer ile ilerlersek son noktaya geldiğimizde de bulduğumuz uzaklık değerleri en düşük değerlerde olacaktır mantığıyla çalışıyor. Oldukça mantıklı, basit ve zarif olan bu yöntem aynı zamanda en verimli algoritma olma özelliğinden dolayı günlük yaşamımızda biz farkında olmasak da sıkça kullanılıyor. Örnek vermek gerekirse, OSPF ve ISIS gibi yönlendirme protokollerinin temel prensibi Dijkstra’nın algoritmasıdır.
Başka bir e-bergi yazısında görüşmek üzere hoşçakalın...