Tüm okuyucularımızı bahar aylarının bu sıcak günlerine girerken yeni sayımızla selamlıyorum. Bu ay geçen ayki yazımın konusuna paralel bir konu seçtim; şöyle bir giriş yaptığımız bilgisayarlı görme konusunun ilgilendiği alanlardan biri olan desen tanıma konseptlerini inceleyeceğiz. Başta karışık görünen bu konu, aslında sadece görüntülerin içinde deneylerle bulunan tekrarlayan yapıları, matematiksel olarak ifade etmeye dayanır. Pratikte çoğu problem görüntülerdeki nesneleri ayırt etmeye ve bunların ait oldukları sınıflara karar vermeye dayanırken, teoride birçok olasılık hesabı bu problemleri temsil etmektedir. Öncelikle konu hakkında bazı tanımlara göz atalım.
Sınıf (class): Bir nesnenin veya yapının türü olarak düşünebiliriz. Önemli benzer özellikleri olan nesnelerin kümesidir. Geçen ay değindiğimiz gibi, kesin çizgilerle belli değildir. Elma ve armut sınıfları olabileceği gibi, bir sandalyenin 7-8 ayrı türünün sınıflandırılması yapılmaya çalışılıyor da olabilir. Sınıf etiketi nesnenin ait olduğu sınıfı belli eder. Sınıflandırma ise, bir nesnenin özellilklerinin gösterimine göre sınıf etiketi atama sürecidir. Son olarak sınıflayıcı ise; girdi olarak nesne özellikleri kümesi alıp, çıktı olarak sınıf etiketi veren bir alet veya algoritmadır.
Desen (pattern): Bir bileşenin sınıfının etiketini taşıyan özellik vektörüdür.
Özellik ayırıcı (feature extractor): Görüntüyü alıp, sınıflandırmada kullanılacak özelliklerini çıkaran programdır.
Doğrulama (verification): Bir nesnenin herhangibir örneğini, belirli bir nesne prototipine veya sınıf tanımına eşleme işlemine denir. Sınıflandırmanın son adımı olarak görülebilir.
Öğrenme (learning): Genellikle hazırlanma kümesindeki görüntüler kullanılarak, sınıfların matematiksel modellerinin bulunmasına denir.
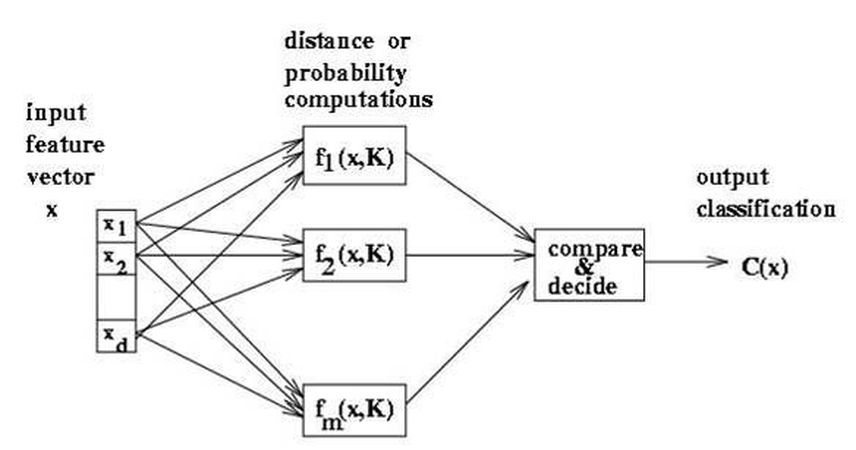
Tanıma (recognition): "Tekrar bilmek" olarak düşünebildiğimiz "tanıma", daha önce oluşturulmuş matematiksel sınıf modelini kullanarak bilinmeyen bir yapıyı veya bileşeni tanıyabilmektir. Bu aşamada öğrenme ve tanıma konseptlerinin oturması çok önemlidir.
Hassasiyet (precision): Bir görüntü sorgusu yapıldığında; getirilen görüntülerin arasındaki sorgu görüntüsüyle ilgili görüntülerin, getirilen görüntülere oranıdır.
Anımsama (recall): Yine bir görüntü sorgusunda; getirilen görüntülerden ilgili olanların sayısının, veritabanındaki tüm görüntülere oranıdır.
Bilgisayarlı Görmede Kullanılan Sınıflayıcılar
Çeşitli nesneleri tanımak için özelliklerini kullandığımızı söylemiştik. Peki bu özellikler neler? Şeklin alanı, çemberselliği, çevresi, merkezinin diğer şekillere uzaklığı, içerdiği girinti çıkıntılar ve bunlar gibi birçok özelliği nesneleri karakteristik olarak belirtmekte kullanabiliyoruz. Ancak sadece numerik veya sembolik özelliklerin yetmediği durumlar da oluyor. Mesela bir nesnenin döndürülmüş hallerini veya simetriklerini ele aldığımızda, bu daha farklı nesnelerin daha belirgin özellikleri olması gerek. Ancak sadece var olan özellikleri kullanarak bu nesneleri ayırt etmemiz neredeyse imkansız. Bu yüzden, sadece yapısal özellikleri kullanmak yerine, bu özellikler arasındaki ilişkiler de kullanılıyor. Yani bu sınıflayıcılar, esasen iki, bir de bileşik grupla birlikte üç gruba ayrılıyor.
İstatistiksel Yaklaşım (Statistical Pattern Recognition)
Görüntü sınıfı, sınıfın özelliklerine karşılık gelen bir rastgele değişken ile belirtilerek, sınıf pdf bulunarak modellenir. Özellik vektörleri ile birimlerin (entity) gösterildiği bu yaklaşımda, özellikler tamamen sayısal ve atomik hale gelmiştir. Bir özellik tüm nesneler için geçerli olan bir ölçü ile sayısal veya Boolean olarak gösterilmektedir. Mesela bir nesnenin sahip olduğu deliklerin sayısını bilmek gibi. İstatistiksel yaklaşım sınıflayıcılarının kullandığı bazı özellikler şunlardır:
- Şeklin alanı (piksel sayısı)
- Şeklin genişliği/uzunluğu (çevreleyen piksel sayısı)
- Şeklin içindeki delik sayısı
- Şekli oluşturan darbe sayısı
- Şeklin ağırlık merkezi
- Şeklin minimum eylemsizlik sağlayan en iyi eksen yönü
Bu özellikleri kullanan sınıflandırma yöntemlerine göz atalım.
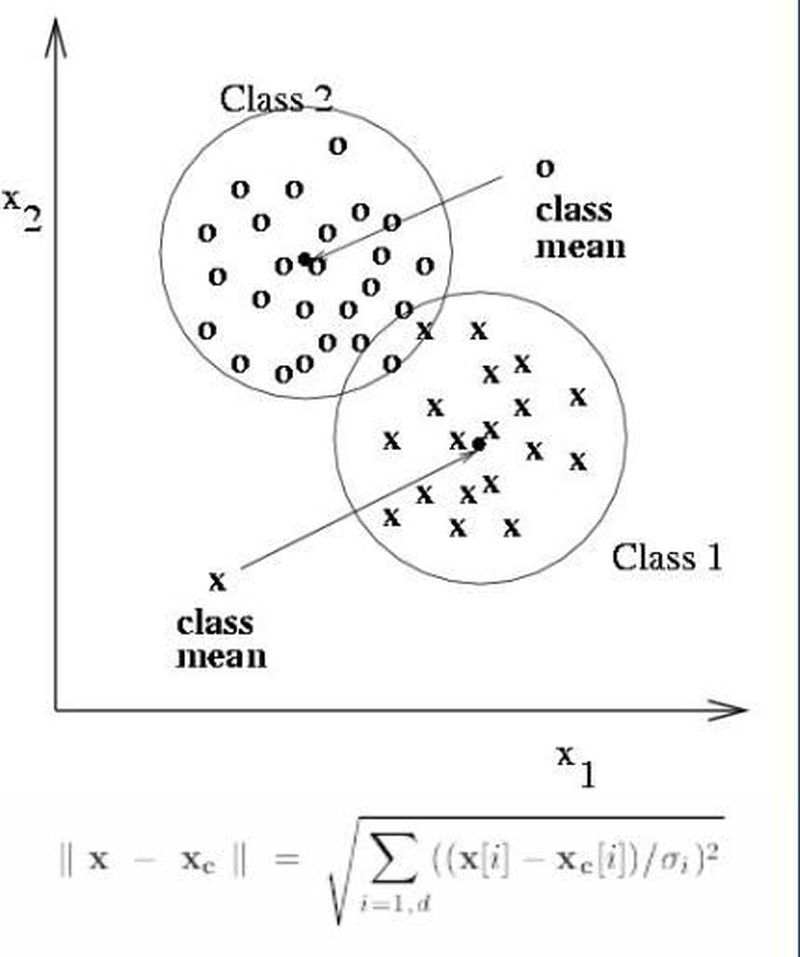
1. En Yakın Sınıf Ortalaması Sınıflandırması (Nearest Class Mean Classification)
Birçok örnek alındıktan sonra, bunların kullanılacak belirgin özellikleri ölçülür. Daha sonra özellik uzayında her bir örnek bir noktayı temsil edecek şekilde işaretlenir. Bu noktalara göre sınıfların ortalamaları belirlenir. Daha sonra herbir yeni bilinmeyen örneğin hangi sınıfa ait olduğu bu sınıf ortalamalarından hangisine daha yakın olduğu hesaplanarak belirlenir. Tek bir özellik kullanıldığında "özellik doğrusu" (özellik histogramı), iki özellik kullanıldığında "özellik düzlemi", üç ve daha fazla özellik kullanıldığında ise "n-boyutlu özellik uzayı" üzerinde bu hesaplamalar yapılır. Uzay kaç boyutlu olursa olsun aradaki mesafe önemlidir. Bu uzaklık da, genel "Öklit uzaklığı" olarak alınabileceği gibi, "Mahalanobis uzaklığı" da kullanılabilir. Bu yeni uzaklığın faydası, sadece merkezlere bakmak yerine, sınıfın yapısına da bakmaktır. Yani artık sınıflarımız sadece çembersel değil, elips şeklinde de olabilmektedir. Uzaklıklar bu yapıya göre ölçeklendirilerek değerlendirilir.
Eğer sınıfların uzayda kapladıkları boşluklarda çok fazla üst üste binme varsa, kullanılan özellikler yeterli değildir. Yani bu ortak alanları azaltmak için başka bir ölçü daha gerekmektedir, bu da başka bir boyut demektir. Böylece ayırt edilebilecek kadar ortak alan azalana kadar, yeni özelliklerle özellik vektörünün boyutu arttırılabilir.
2. En Yakın Komşu Sınıflandırması (Nearest Neighbourhood Classification)
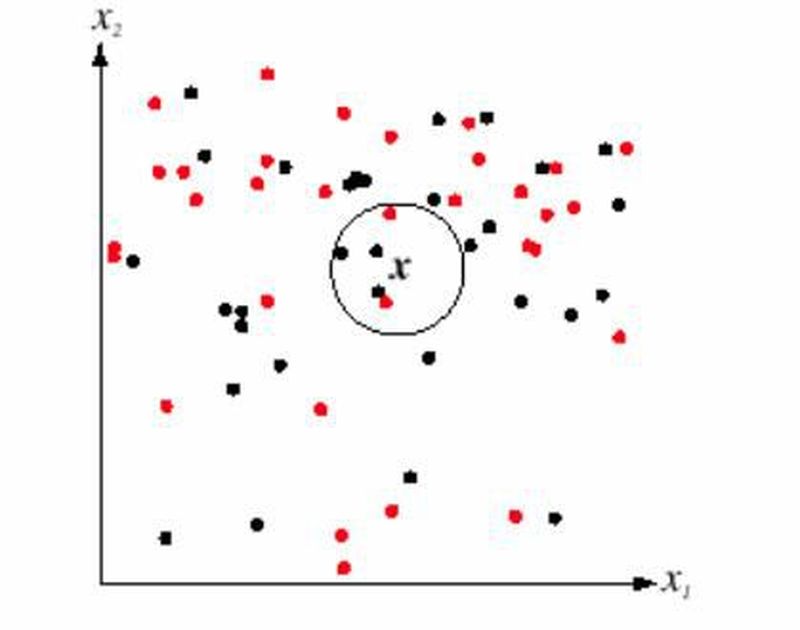
Bu diğerine göre daha esnek ama daha pahalı bir yöntemdir. Sınıflar çok fazla örtüştüğünde ve dağınık bir dağılım olduğunda daha kullanışlıdır. Bir örneğin, en yakın K komşusunda en sık görülen sınıfın etiketini alması kuralına dayanır. Ancak bunun için hazırlanma evresi çok uzundur.
Veri kümemizin bütün örneklerinin sınıf etiketlerini bildiğimizi düşünelim. Her seferinde, bir örneğin sınıfını bulmaya çalışarak, K'nın her değeri için performansı gözlemliyoruz. Bunu her örnek için tekrarladığımızda, K'nın hangi değeri için en doğru sonuç aldıysak, o değeri kullanıyoruz. Bu yüzden K değerinin bulunması hazırlık sürecindeki hazır verilerimizle oluyor, bulunduktan sonra esas sınıflandırmaya geçiyoruz. Bu işleme de "One leave-out cross validation" deniyor.
3. Bayes Sınıflandırması (Bayesian Classification)
Elimizde yine hazırlık verileri olduğu için, bir x örneğinin, bir w<sub>i</sub> sınıfına ait olma olasılığını hesaplamak istiyoruz; çünkü olasılığı maksimum hale getirmeyi sağlıyor. Ayrıca Bayes bu yöntemiyle öğrenme ve hazırlık aşamalarını tek bir adımda birleştirmeyi bulmuştur. Bu olasılık hesabı için kullandığımız üç değer var:
- Koşulsal sınıf dağılımı: tüm sınıflar için hesaplanan, w<sub>i</sub> sınıfındayken örneğimin x olma olasılığı = P(x|w<sub>i</sub>) (yani her sınıfın kendi içinde histogram dağılımı)
- Önsel olasılık: yine tüm sınıflar için hesaplanan, bir sınıfın olasılığı = P(w<sub>i</sub>)
- Koşulsuz dağılım: örneğimizin x özelliğini taşıması olasılığı = P(x)
Bu verileri kullanarak vardığımız sonuçsal olasılık:
P(w<sub>i</sub>|x) = P(x|w<sub>i</sub>)*P(w<sub>i</sub>)/p(x) = P(x|w<sub>i</sub>)*P(w<sub>i</sub>)/[sum of all P(x|w<sub>i</sub>)*P(w<sub>i</sub>)]Ancak amacımız karşılaştırma olduğu için, formülün bölen kısmı tüm örnekler için aynı olduğundan, sadece payları karşılaştırarak da sonuca ulaşılabilir.
Yapısal Yaklaşım (Structrual Pattern Recognition)

Yapısal yaklaşımda ise bir birim basit kısımları, onların özellikleri ve aralarındaki ilişkilerle ifade edilir. İki koyu olan bir karakteri tanımak için istatistiksel yaklaşım kullanıldığında, hem "H" hem de "E" harfi anlaşılabilirken; yapısal desen tanımada "H"deki koylar birbirinin üstündeyken (Above relation), "E"dekiler birbirine komşudur (Adjacent relation). Bu yüzden böyle bir örnekte yapısal yolun kullanılması daha pratiktir. Bu ilişkiler bir grafik yapısı ile gösterilebilir, bu yüzden yapısal desen tanıma çoğunlukla grafik eşleşme algoritmaları kullanılarak yapılır. Gramerlerden de gösterim için yardım alınır.
Hazırlık aşamasında görüntü basit işlemlerden geçirilerek özellikleri güçlendirildikten sonra, kenar, köşe, göl, koy, delik, vb. şekilleri çıkartılır. Daha sonra bunların arasındaki ilişkiler (üstünde, komşu, bağlı, vb.) çıkarılarak, her sınıf ayrı bir grafik üzerinde gösterilir. Tanıma kısmında ise, grafik benzerlikleri kullanılarak (grafik izomorfizmi mesela) sınıf etiketi atanır.
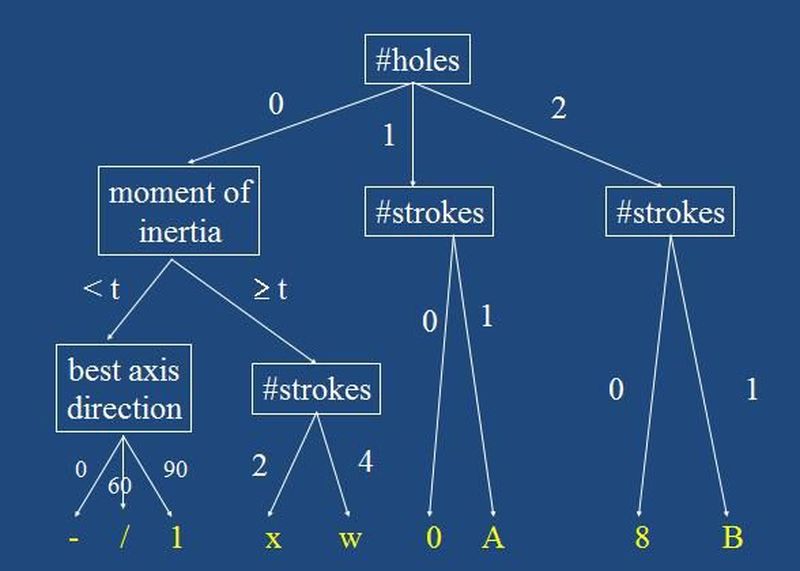
1. Karar Ağaçları (Decision Trees)
Desen tanıma işlemi birçok özellik kullanıldığı için çok karmaşık olduğunda, tamamen farklı iki özellik vektörünü karşılaştırmak çok zaman alıcı olabilir. Bunun gibi durumlarda, karar ağaçları kullanılarak, arama uzayının sürekli bölünmesi sağlanarak karşılaştırma işlemi kolaylaştırılır. Mesela bir düğümde "yapıdaki delik sayısı" olsun, çocuklarında da diğer özellikler. Bu düğümün ilk çocuğuna sıfır delikli ise, ikinci çocuğuna bir delikli ise, üçüncü çocuğuna ise iki delikli ise gidebiliyoruz. Böylece bir kerede denenecek olasılıkları 1/3üne indirebiliyoruz. İyi bir karar ağacı olabildiği kadar dengede, tanım kümesi iyi seçilmiş, kenarları düzenli, hazırlık verilerinden analizle oluşturulmuş, bilgi içeriğine uygun olarak en fazla olan köke yerleştirilmiş olmalıdır.
Bunun dışında bir de ikili karar ağaçları vardır. Düğümlerde soru bulunurken, sol çocuğa "evet" cevabı, sağ çocuğa da "hayır" cevabı gider.
Hem Yapısal Hem İstatistiksel Yaklaşım
Yapay Sinir Ağları (Artificial Neural Networks) bu sınıflandırmanın örneğidir. Biyolojiden esinlenilmiş sistemlerdir. Özellikleri girdi olarak farklı ağırlıklardaki dendritlerden alan nöron, çıktı olarak nesnenin ne olduğunu verir. Ancak nöronun bu karar işlemi tamamen öğrenmeye dayalıdır. Çünkü hazırlık fazında hem nöronun fonksiyonu hem de ağırlıklar, ne verilirse verilsin doğru sınıfı verecek şekilde ayarlanmaktadır. Ayrıntılı bilgiyi Yapay Sinir Ağları yazımızda bulabilirsiniz.
Performans?
Bütün bu yöntemlerin hangisini kullanacağımıza nasıl karar vereceğiz peki? Bunun için de farklı veri kümelerine ve farklı işlevlere göre performans analizi yapan yollar bulmuşlar. Kısaca bunlara da değinelim.
Sınıflandırma Oranı Çok basit bir frekans bulmaya dayanır:
sınıflandırma oranı = w<sub>i</sub> sınıfındaki doğru tahmin edilmiş örnekler/ toplam örnek sayısı
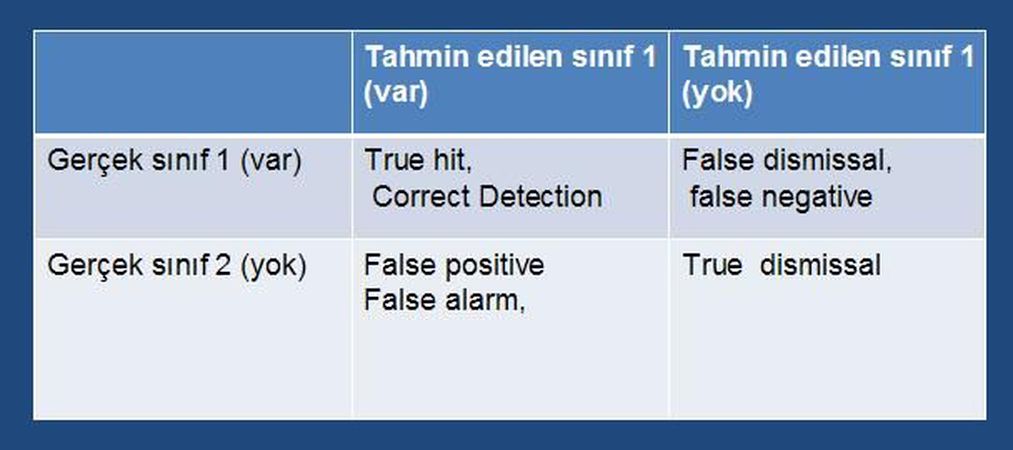
3. Sınıf Problemi Sınıf sayısının karesi kadar hücresi olan bir tabloda, şekildeki gibi elde edilen verilerdir. Bunlardan "true hit "(doğru tahmin) en olması gerekeni, "true dismissal" (doğru ama diğer sınıf) zararsız olanı, "false alarm" olanı nispeten yanlış bilinmesine göre zararsız olanı, "false dismissal" da bir o kadar ölümcül olanıdır. Güvende olmak için yanlış alarm oranını çok yüksek tutarak hit oranını yükseltebiliriz. 4. Alıcı İşleten Eğri Doğru bilinen orana karşı yanlış alarm oranını çizer. Genelde, yanlış alarmlar, bilinen nesneleri daha sık bulmaya çalışma denemelerine göre artar. Ayrıca bu eğri ne kadar düzgün ise o kadar benzerlerdir. Bu eğriler hassasiyet ve anımsama ile de ilgilidir. 5. Karışıklık Matrisi (Confusion Matrix) Tahmin edilen sınıflara karşı, gerçek sınıfların bulunduğu bir grafiktir. Dolayısıyla ne kadar köşegende birikme olursa, o kadar performans yüksektir.
Sanırım bu ayki yazımın da sonuna geldim. Gelecek ay yepyeni bir sayıda buluşmak dileğiyle...