Merhaba sevgili e-bergi okurları, yeni bir sayımızla tekrar karşınızdayız. Bu yazımda sizlere B+ ağaçlarından bahsedeceğim. B+ ağaçlarının hem algoritmik yapısı hem de algoritmik özellikleri hakkında sizleri bilgilendirmeye çalışacağım.
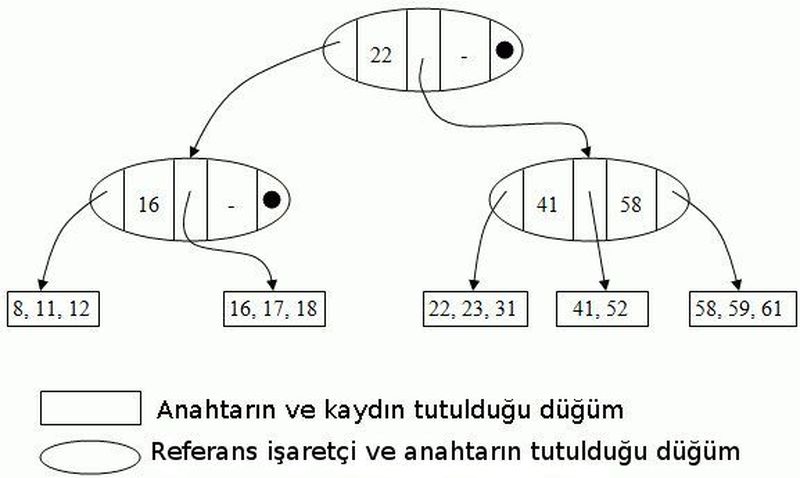
B+ ağacı, sıralanmış halde bulunan veriye yeni veri eklerken, bu veriden eksiltme yaparken veya sadece veriye ulaşmak istediğimizde hızlı ve verimli bir şekilde ulaşmak için sıkça tercih edilen, indeksleme amacıyla kullanılan bir ağaç yapısıdır. İndeksleme her bir veride bulunan ve sadece o veriye özel olan (yani her bir veri için farklı olan) bir değeri seçerek yapılır. Bu değere anahtar denir. B+ ağaçları sahip olduğu verilerin ya da anahtarların sayısına bağlı olarak büyüyüp küçülebilir. Bu yüzden, dinamik bir yapıya sahip olan B+ ağaçlarının yüksekliği değişkendir; ancak ağaca ekleme ve çıkarma yaparken kullanılan algoritmaların dizaynı -dolayısıyla tüm yapraklar- aynı yüksekliktedir ve bütün kayıtlar yaprak düzeyinde tutulur. Sadece anahtarlar yaprak olmayan noktalarda tutulur. B+ ağaçlarının her bir indeks parçasındaki (blok veya düğüm noktası olarak da adlandırılır) anahtar sayısı bir maximum ve bir minimum değer ile sınırlandırılmıştır. Bu minimum sayıya ağacın derecesi denir ve bir düğümde bulunabilecek maximum anahtar sayısı minimum anahtar sayısının iki katıdır. B+ ağaçlarını normal bir ikili ağaçtan ayıran en önemli özellik, derecesinin (dolayısıyla sahip olduğu işaretleyicilerin sayısının) yüksek olabilmesidir. Bu sayede, yapılacak bir operasyonda disk okumaları minimize edilmiş oluyor ve fazla sayıdaki verilerde bile algoritma yüksek hızda çalışabiliyor. Btrfs, NTFS, ReiserFS, NSS, XFS ve JFS gibi dosya sistemleri de bu ağaç yapısını kullanıyor. IBM DB2, Informix, Microsoft SQL Server, Oracle 8, Sybase ASI, PostgreSQL, Firebird ve MySQL gibi ilişkisel veritabanı yönetim sistemleri de tablo indeksleri için bu ağaç yapısını desteklemektedir.
Doğal olarak, bu ağaçta yapılan 3 önemli operasyonun (arama, yeni kayıt ekleme ve kayıt çıkarma) nasıl işlediğini anlatmadan önce ağacın genel yapısından bahsetmem gerekir. Ağaçta kayıtların sıralı olduğunu söylemiştik; yani kayıtların tutulduğu düzeydeki (yaprak düzeyinde) tüm düğümler hem kendi içinde hem de birbirlerine göre sıralı. Birbirlerine göre sıralı olması iki düğümden birinin içindeki tüm elemanların, diğerinin içindekilerden küçük anahtar değere sahip olduğu anlamına geliyor. Buradan da çıkarabileceğimiz gibi anahtar olarak seçtiğimiz değerlerin birbirleriyle kıyaslanabilir olması gerekiyor. Sayılarda, doğal olarak, büyüklük küçüklük ilişkisi kullanılırken yazılarda alfabetik sıralama göz önünde bulundurulur. Aslında tüm düğümlerde anahtarlar aynı şekilde sıralı halde tutulur. Anahtarların her birinin önünde ve arkasında bir alt seviyedeki düğümleri gösteren işaretleyiciler vardır. Alttaki düğümler zaten sıralıdır ve onu gösteren işaretleyicinin solundaki anahtarın değeri, alttaki düğümdeki minimum değere sahip anahtarın değerinden küçük veya ona eşittir. Benzer şekilde işaretleyicinin sağındaki anahtar değeri de işaretlenen düğümdeki tüm anahtar değerlerinden büyüktür. Eğer düğümün başındaki veya sonundaki işaretleyiciler söz konusuysa -yani solda veya sağda herhangi bir anahtar değer bulunmuyorsa- o düğümü gösteren işaretleyicinin sağındaki veya solundaki değere bakılır. Ebeveyn düğümlere bakma işlemi, bulunamayan her anahtar değer için kendini tekrar ederek yapılır; fakat sonunda bir değere ulaşılamıyorsa ve ilk baktığımız anahtar düğümün en başındaysa bu, o düğümün bir alt sınırının olmadığını gösterir. Benzer şekilde düğümün en sonundaysa da bu, o düğümün bir üst sınırının olmadığını ifade eder.
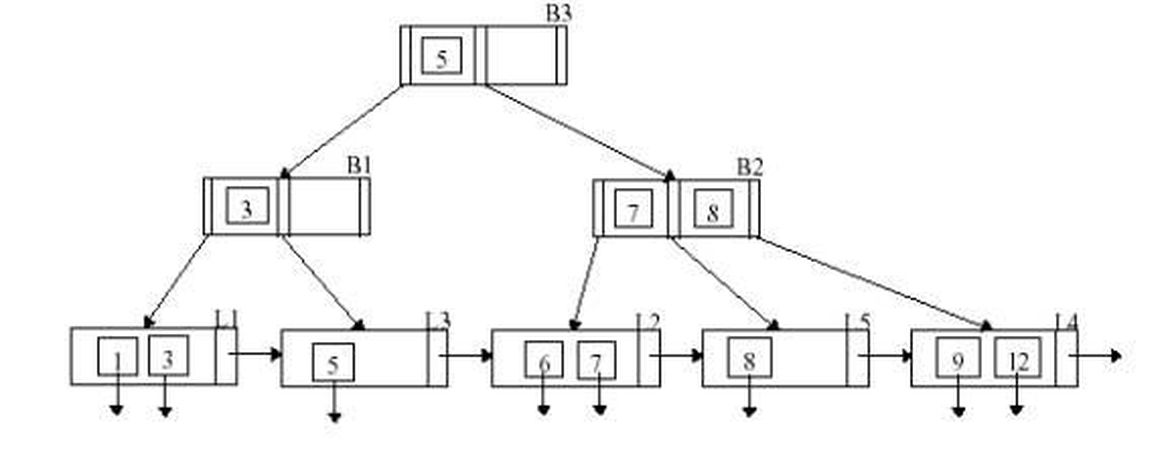
B+ ağaçlarının yapısını öğrendiğimize göre artık anahtarı verilmiş bir düğümü aramak için yapılması gerekenleri inceleyebiliriz. Arama algoritması şu şekilde işlemektedir:
- Kök düğümü bakılan düğüm olarak seçilir.
- Bakılan düğüm bir yaprak değilse;
- Bakılan düğümde aranan kaydın anahtar değerine göre arama yapılır.
- Aradığımız anahtar değerden küçük olan en yüksek değerli anahtardan sonraki işaretleyicinin gösterdiği düğüme gidilir.
- Bu düğüm bakılan düğüm olarak seçilir.
- 2. adıma geri dönülür.
- Bakılan düğüm bir yaprak ise aradığımız düğüm ya bu yaprak düğümdedir ya da bizim kayıtlarımız arasında yoktur. Bu yüzden son olarak bu düğümde bir arama yapılır ve aradığımız düğümü (veya cevabı :) ) bulmuş oluruz.
Artık kayıt eklerken veya silerken kullanılan algoritmaları anlatırken “Doğru yaprak düğüm (veya kısaca düğüm) bulunur.” gibi cümleler kurduğumda, yukarıdaki arama algoritmasının takip edildiğini varsayabilirsiniz. Ekleme algoritması şu şekildedir:
- Yeni eklenecek kaydın anahtar değerine göre, olması gereken düğüm bulunur.
- 2.Eğer bu yaprak düğüm, derecesinin iki katından daha az kayıt tutuyorsa; yani düğümde boşluk varsa kayıt, düğüm içinde sırayı koruyacak şekilde doğru yere eklenir. (ve burada algoritma bitmiş olur.)
- Boşluk yoksa düğüm ikiye ayrılır.
- Yeni bir yaprak oluşturulur ve düğümdeki elemanların yarısı, sıralanmış hali bozmadan bu yeni yaprağa eklenir.
- Yeni düğümdeki en küçük elemanın anahtar değeri ve adresi ebeveyn düğüme eklenir.
- Eğer ebeveyn düğüm doluysa o da ikiye ayrılır.
- Sonra onun ortasındaki anahtar sadece yukarıya kaydırılır. (yani onun ebeveynine geçer ve yaprak düğümlerden farklı olarak kopyası aşağıda kalmaz)
- Bu işlem bölünme gerektirmeyen bir ebeveyn düğüm bulunana kadar tekrar eder.
- Eğer en son kök düğümü de ikiye bölünürse tek bir anahtar değeri ve iki işaretleyicisi bulunan yeni bir kök düğüm oluşturulur. (B+ ağaçlarında tüm düğümlerdeki anahtar sayısı derece ve derecenin iki katı arasındadır; ancak kök düğüm buna istisnadır. Kökte, birden derecenin iki katına kadar herhangi bir sayıda anahtar bulunabilir.)
Anahtarı verilmiş bir kaydı silmek için ise şu yol izlenir:
- Anahtarı verilen kayıt, yaprak düğümler arasından bulunur.
- Düğümde tutulan kayıtlar ağacın derecesine eşit veya ondan büyükse silme işlemi gerçekleştirilir.
- Daha az kayıt varsa (Bu, kök düğüm dışında, her zaman dereceden bir eksik adette olduğu anlamına gelir) yanındaki -aynı ebeveyne sahip- düğümden ödünç alınıp bu düğüme eklenir. Bu işleme tekrar dağıtma denir.
- Eğer tekrar dağıtma başarısız olursa; yani kardeş düğüm de derecenin altında kayda sahipse, iki düğüm birleştirilir.
- Birleştirilme yapıldıysa sağdaki düğümü gösteren işaretleyici ve onun anahtarı ebeveynden silinir. Bu durumda ebeveyn de anahtar sayısını azalırken o da aynı şekilde kök düğüme kadar silme operasyonuna tabi tutulur.
B+ ağaçlarının operasyonlarındaki algoritmaları öğrendiğimize göre artık özelliklerine geçebiliriz.
Ağacın derecesini d, yüksekliğini y ve eleman sayısını da n ile gösterirsek, bir B+ ağacı için şunları söyleyebiliriz:
En fazla n = (2d)<sup>y</sup> kayıt tutulur,
En az 2d<sup>y-1</sup> anahtar bulunur,
Ağacı tutmak için gerekli olan yer miktarı O(n)'dir.
Yeni bir kayıt eklemek en kötü durumda O(log<sub>d</sub>n)'dir.
Bir kaydı aramak en kötü durumda O(log<sub>d</sub>n)'dir.
Bir kaydı silmek en kötü durumda O(log<sub>d</sub>n)'dir.
Belli bir aralıkta k adet elemanla sıralama yapmak en kötü durumda O(log<sub>d</sub>n + k) kadar işlem gerektirir.Sonuç olarak B+ ağaçları, biraz karmaşık yapısına rağmen sağladığı faydalar sayesinde sıkça tercih edilen bir indeksleme yöntemidir. Özellikle büyük miktardaki verilere ulaşmakta sağladığı hız onu, diğer birçok yöntemin arasında ön plana çıkarmaktadır. Bir sonraki yazıda görüşmek üzere, hoşçakalın.