Bu ay da yeni sayımızla sizinle birlikteyiz. Ben de çok kullanılan veri yapılarından biri olan AVL ağacını ve uygulamalarını anlatmaya çalışacağım. İlk olarak bu veri yapısının tanımıyla başlayalım; AVL ağacı, denge şartı olan ikili arama ağacıdır. AVL ağacının ismi ise onu geliştiren Andelson-Velsky ve Landis'in isimlerinin baş harflerinden gelir. Bu veri yapısının önemi ise verimliliğinden kaynaklanmaktadır. Düğüm sayısı n olan bir ağaçta düğüm arama, yeni düğüm ekleme ve düğüm silme işlemlerinin ortalamada ve en kötü durumda O(log n)lik zaman alır ve ideal ağaca yakındır (tamamen dengeli ağaç).
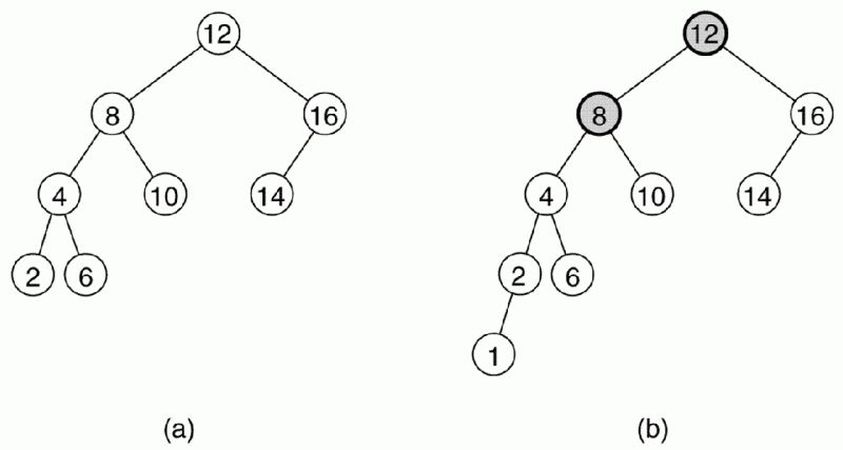
İkili arama ağacında her kökün sol çocuğu olan ağaçtaki bütün düğümler kökten küçük, sağdakilerse kökten büyük olmak zorundadır. Bu sayede ikili arama ağacında düğüm arama bir dizide aramaktan daha verimli olur, ortalamada O(log n) zaman alsa da ağaç dengeli bir biçimde dağılmadığı zaman O(n)e yaklaşır. Bu sorunu ortadan kaldırmak için AVL ağacını kullanabiliriz. Herhangi bir ikili arama ağacının AVL ağacı olmasının şartı ise bütün düğümlerin çocukları arasındaki yükseklik farkının en fazla bir olmasıdır. Resimdeki (a) ağacı AVL yapısına uygundur. Ama diğer ağaçta 8'in ve 12'nin çocukları arasındaki yükseklik farkı 2dir ve bu nedenle (b) ağacı AVL ağacı değildir.
AVL ağacının önemli işlemleri ağacı dolaşma, yeni düğüm ekleme, düğüm arama, düğüm silme ve ağacı tekrar dengelemek için kullanılan döndürmelerdir.
Düğüm arama AVL ağacında yeni düğüm eklemede ve düğüm silmede de kullanıldığı için en çok kullanılan işlemlerden biridir. AVL ağacı dengeli ikili arama ağacı olduğu için en kötü durumda ve ortalamada O(log n)lik zaman alır. Aranan düğüm köke eşitse düğüm bulunmuştur, eğer küçükse kökün sol çocuğuna geçilir, büyükse sağ çocuğuna. Bu işlem düğüm bulunana ya da en son yaprağa (leaf, çocukları olmayan düğüm) bakılana kadar devam eder.
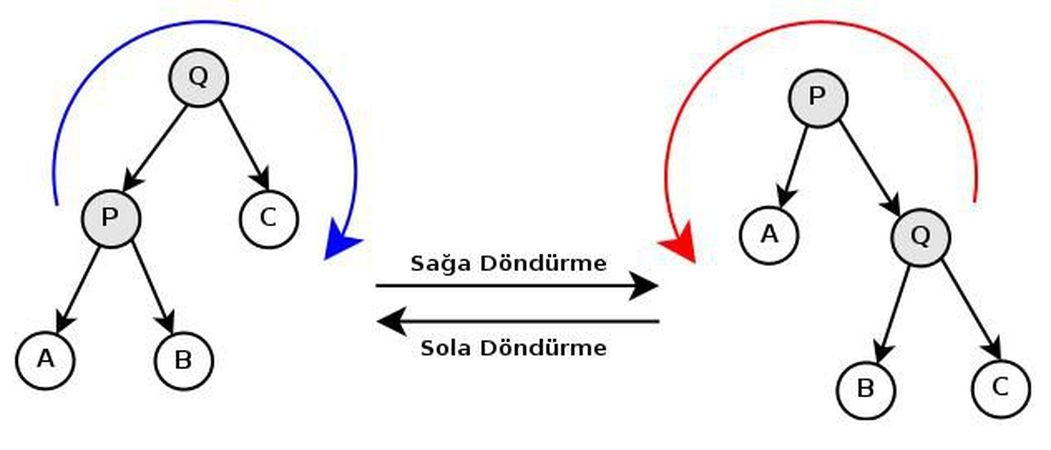
AVL ağacına yeni bir düğüm eklemek için ilk önce eklenecek düğüm ağaçta varmış gibi aranır ve yeni düğümün ekleneceği düğüm bulunur. Bu şekilde ağaç, ikili arama ağacı yapısına uymuş olur, ama AVL ağacının diğer şartı olan dengeye de bakılmadır. Yeni eklenen düğümden köke olan yoldaki düğümlerin dengesini kontrol etmek yeterlidir. Yeni oluşan dengesizlik durumu dört şekilde olabilir ve dengeyi yeniden sağlamak için döndürmeler yapılır. İlk olarak düğüm sol çocuk olan ağacın sol koluna eklenmişse sağa döndürme yapılır. İkinci durum da bunu simetriğidir; sağ çocuk olan ağacın sağ koluna eklenen düğüm için sola döndürme gerekir. Resimde P ve Q düğümleri arasında sağa ve sola döndürme yapılmıştır. Yapılan tek döndürmelerle ağacın yüksekliği korunmuştur. Yeni eklenen düğümden köke kadar olan yolda dengenin bozulduğu ilk düğümde döndürme yapıldı için ağacın dengesi korunmuş olur. Döndürme işlemi O(1), ve dengenin bozulduğu düğümü bulmak O(log n)lik zaman aldığı için bu işlem O(log n)lik bir algoritmadır. Üçüncü ve dördüncü durumlarda ise çift döndürme gerekir. Üçüncü durumda sağ çocuk olan ağacın sol koluna yeni düğüm eklenmesiyle oluşur ve bunu için sol-sağ döndürmesi yapılmalıdır. Dördüncü durum da bunun simetriği olup problemli düğümlerde sağ-sol döndürmesi yapılır.
Düğüm silme ise eklemeden biraz daha karışık, birden fazla dengeleme işlemi gerektirebilir. Bu algoritma da yeni düğüm ekleme gibi O(log n)lik zaman alır ve eklemede kullanılan tek ve çift döndürmelerin yanında denge faktörü de kullanılır. Denge faktörünün bir düğüm için üç durumdan birini göstermesi gerekir: sol çocuğun yüksekliğinin sağ çocuğun yüksekliğinden fazla olması, az olması ve eşit olması. İlk olarak silenecek olan düğüm bulunur, bu da O(log n)lik zaman alır. Silinecek olan düğüm bulunduktan sonra düğüm yapraksa silinir, değilse düğümden önceki ilk yaprakla (silinen düğümden küçük olan en büyük yaprak) yerleri değiştirilip, düğüm silinir. Dengeyi kontrol etmek için ağacın boyunun kısalıp kısalmadığını tutan, ilk değeri true olan bir Boolean değişkeni kullanmamız gerekir (shorter). Eklemede olduğu gibi silinen düğümden köke kadar olan bütün düğümlerin dengeleri kontrol edilmelidir ve bunun için de shorter değerine, denge faktörüne bakılmalıdır. Shorter false olduğunda da bu kontrol algoritması sonlanır. Bir düğümün denge kontrolünde üç değişik durumla karşılaşılabilir. İlk olarak silinmeden önce düğümün denge faktörü eşitse; düğüm silindikten sonra denge faktörü güncellenir, shorter false yapılır. Ağacın boyu değişmediği için ağacın AVL yapısını değişmemiştir, dönüşlere gerek olmaz. İkinci durumda ise yüksekliği fazla olan çocuktan düğüm silinir. Bu işlemden sonra düğümün iki çocuğunun yüksekliği eşitlenmiş olur ve denge faktörü güncellenir. Ancak ağacın boyu kısaldığı için shorter true yapılır. Bu değişiklik, düğümün ebeveynini etkileyeceği için kontrole ebeveyn olan düğümle devam edilir. Son olarak da denge faktörü eşit değildir ve düğüm de kısa olan ağaçtan silinecektir. Bunun için de üç durum söz konusudur. İlk olarak uzun olan çocuğun denge faktörü eşittir(çocukları arasında yükseklik farkı yoktur). Tek dönüş gerekir ve dönüş sonunda ağacın boyu değişmediği için shorter false olarak güncellenir. Eğer uzun çocuğun denge faktörü ebeveynininkiyle aynıysa tek döndürme yapılır ve ağacın boyu değiştiği için shorter true yapılır ve kontrole ebeveynle devam edilir. Son durumda ise yüksekliği fazla olan çocuğun denge faktörüyle ebeveynininki zıttır ve çift döndürme gerektirir. Döndürmeler sonucu düğümlerin denge faktörleri güncellenir. Ağacın boyu kısaldığı için shorter true yapılır. Kontrol algoritması shorter false olduğunda ya da AVL ağacına kökü kontrol edildiği zaman sonlanır. Siz de yeni düğüm ekleme, düğüm silmeyi bu adresteki uygulamayla deneyebilirsiniz:http://webpages.ull.es/users/jriera/Docencia/AVL/AVL%20tree%20applet.htm
Düğüm sayısı n olan bi AVL ağacının yükseklik limiti (1.44*log n)dir. Ağacı dolaşmak ise bütün düğümlere bakılacağı için O(n)lik zaman alır.
Uygulamada zorlukları olsa da avantajlarından vazgeçemeyeceğimiz AVL ağaç yapısını ve bu yapıyla kullanılan işlemleri anlatmaya çalıştım bu sayımızda. E-bergiyle kalmanız dileğiyle...