Merhaba değerli e-bergi okurları! Bu yazımda sizlerle bilgisayar bilimlerinde önemli yer tutan keşifsel yaklaşımlardan olan A* yönteminden bahsedeceğim.
Yöntemi açıklamaya geçmeden önce keşifsel yaklaşımlardan biraz bahsedip onların alanımızda neden gerekli olduklarından bahsetmek istiyorum. Keşifsel yaklaşımlar özellikle bilgisayar bilimleri, yapay zeka ve matematiksel optimizasyon gibi alanlarda çözülmeye çalışılan problemin büyüklüğü çok fazla olduğunda, ortalama çözüm süresinin üstel olduğu durumlarda ya da klasik yöntemlerin bir çözüm bulmayı başaramadığı durumlarda kullanılırlar. Bu tip problemlerde zaman zaman çözüm hızını arttırabilmek için en doğru çözümü bulma isteği feda edilebilir. Aslında bilgisayar bilimleri alanının büyük bölümünde de en doğru çözümü bulmak mümkün olmadığından, yeterince iyi çözümü bulmak da yeterli olmaktadır. Bu sebeple keşifsel yöntemler ile geliştirilen çözümler gerçek uygulamalarda çok büyük yer tutmaktadır. Bu gün de o keşifsel yöntemlerden biri olan A* çizge tarama yöntemini öğreneceğiz.
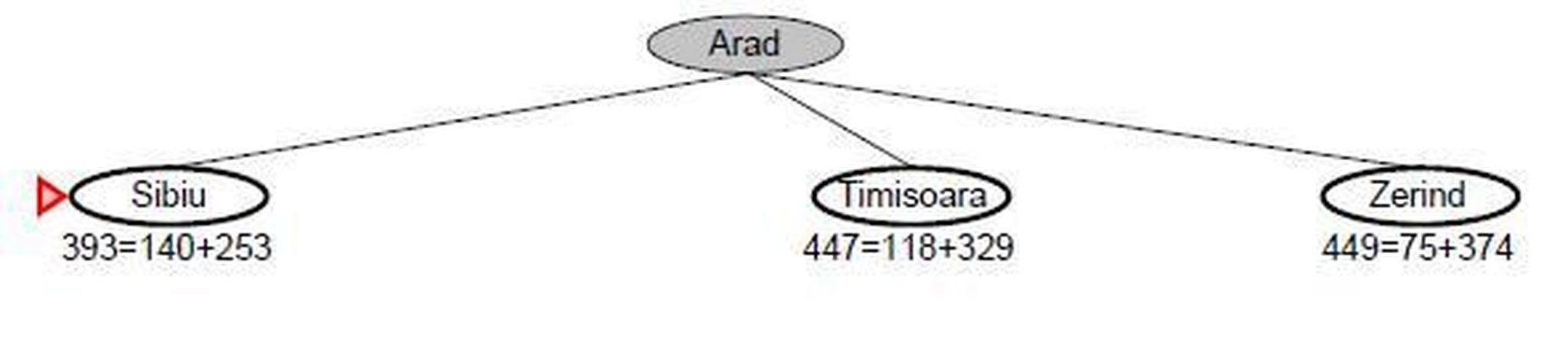
A* yöntemi bir çizge tarama yöntemidir. Çizgenin ilk düğümü problemin başlangıçtaki durumu olmak üzere, her adımda bir adım sonraki olası durumlar hesaplanır ve her biri yeni bir düğüme yazılır. Her adımda elimizdeki tüm düğümler içinden değeri bizim için en uygun olan düğümü seçerek alt düğümlere doğru ilerleriz. Eğer bir düğümde ulaşmaya çalıştığımız hedef durum ile karşılaşırsak problemimizin çözümüne ulaştığımız için yöntem sonlanır. Aslında bu anlatılan işleyiş sıradan çizge tarama yöntemleriyle tamamen aynıdır. İşlemi farklı kılan şey ise bir sonraki adımın ne şekilde seçildiğidir. Klasik yöntemlerde belli bir k derinliğindeki düğüm ile k+1 derinliğindeki düğümler arasındaki değer farkı sabittir; ancak bu yöntemde aynı derinlikteki 2 düğümün değeri farklı olabilir. Daha net açıklamak gerekirse düğümleri bir sonraki derinliğe götüren kenar uzunlukları değişebilir. Yöntem üzerinde daha da ilerlemeden önce şekil 1’de şimdiye kadar anlattıklarımızın üzerinden geçmek yararlı olacaktır. Şekil 1’deki çizge de Arad şehri çizgemizin başlangıç düğümünü göstermektedir. Bir sonraki derinlikte olası bir sonraki şehirler olan Sibiu, Timisoara ve Zerind görünmektedir. Şekilde de görülebildiği gibi aynı derinlikte olan bu şehirlere çizgemizde 253, 329,324 gibi farklı kenar uzunlukları ile ulaşılabiliyor.
Problemimizin en kısa uzaklık problemi olduğunu düşünürsek, her adımda elimizdeki düğümlerden en iyisini seçeceğimizden, bu adımda seçilecek olan düğüm Sibiu’dur. Ayrıca dikkat edilmesi gereken bir nokta da, eğer elimizde farklı derinlikte düğümler olsaydı derinliğine bakmaksızın değeri minimum olan düğümü seçeceğimizdir.
A* yönteminin bir sonraki adımı seçme konusundaki farklılığı ise keşifsel değerler kullanmasıdır. Bir sonraki derinlikteki düğümlerin değerleri hesaplanırken iki düğüm arasındaki kenar uzunluğunun yanı sıra gidilecek olan düğümün hedef düğümünden yaklaşık uzaklığı da kullanılır. Yöntemi keşifsel yapan şey de bu tahmini değerlerin kullanılmasıdır. Matematiksel bir gösterimle iki düğüm arasındaki uzaklık g(x) ve her düğümün hedef noktasına olan uzaklığı da h(x) fonksiyonu kullanılarak bulunabilir. Değerlendirmemizi ve bir sonraki düğüm seçimimizi ise bunların birleşimi olan f fonksiyonuna göre yaparız. f fonksiyonu g(x) ve h(x) değerlerinin toplamı ile hesaplanır. Peki bir düğümün hedef düğümüne olan tahmini uzaklığı nasıl hesaplanabilir ? Bu problemden probleme değişen bir hesaplama yöntemidir. Şayet 2 şehir arasındaki en kısa yolu bulma problemini çözüyorsak, her düğümdeki tahmini uzaklık o şehrin hedef şehrine olan kuş uçuşu uzaklığı olarak hesaplanabilir (o şehrin hedef şehrine olan uzaklığı kuş uçuşu olan uzaklık kadar olmak zorunda değildir).
Yöntemin nasıl çalıştığını ve tahmini uzaklıkların az önceki yaklaşımımıza göre neler değiştirdiğini Şekil 2 ile inceleyelim.
Şekil 2’de -Şekil 1'e ek olarak- şehirlerin değerlerini hedef şehirlere olan tahmini uzaklıları (140,118 ve 75) da toplayarak hesapladık. Seçimimizi yaptığımız düğüm bu durumda değişmedi; ancak eğer Sibiu’nun hedef şehre olan uzaklığı (tahmini uzaklığı) daha fazla olsaydı değişebilirdi. Bu şekilde her adımda bizim için en iyi olan düğümü seçerek hedef şehire ulaşabiliriz.
A* çizge tarama yöntemini farklı kılan şey ise bu yöntemle bulunan yollar her zaman en kısa yollardır; yani A* yöntemi bize en iyi sonucu dönebilen bir keşifsel yöntemdir. A* yönteminin en iyi sonucu dönmesi için tek koşul, her adımda kullandığı tahmini uzaklık fonksiyonlarının onanır bir fonksiyon olmasıdır. Onanır fonksiyonlar, tahmini değerin gerçek değerden her zaman daha düşük fonksiyonlardır; yani gidilecek yolu asla büyütmemelidir. Kuş uçuşu mesafe onanır bir fonksiyondur; çünkü bize her zaman gidilebilecek en kısa yoldan daha kısasını verecektir. A* yönteminin doğru sonucu vermesi için bir diğer koşul, kullanılan f fonksiyonunun da tutarlı bir fonksiyon olmalıdır, yani -negatif uzunlukta bir yol alınamayacağı için- f değeri her zaman büyüyerek gitmelidir. Aksi sonuçlar veren f fonksiyonları kullanılarak oluşturulan A* yöntemleri doğru sonucu bulmayı garanti etmeyecektir. f fonksiyonunun tutarlı olması, h fonksiyonunun tutarlı olmasına bağlıdır.
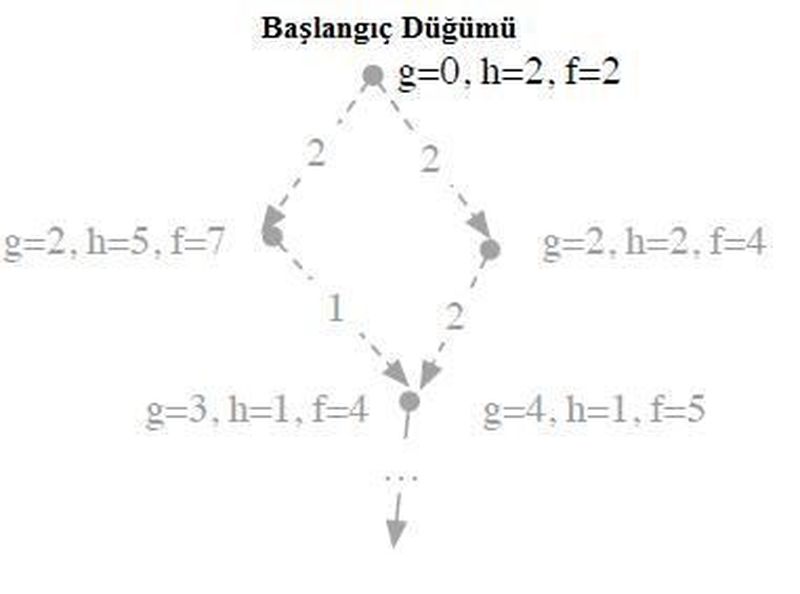
Tutarlı olmayan bir h fonksiyonuna şekil 3’de bir örnek gösterilmiştir. Şekil 3’de h fonksiyonunun tutarsız olduğunu f fonksiyonunun önce 7’ye yükselip daha sonra 4’e düşen değerlerinden anlamak mümkündür. Tutarlı bir fonksiyonda f değerleri alta indikçe artmalıdır.
Sonuç olarak A* çizge tarama yöntemi uygun şartlar altında kullanıldığında hem son derece hızlı hem de tamamen doğru sonuçlar veren bir yöntemdir ve hız gerektiren tarama problemlerinde seçenekleriniz arasına A* yöntemini de koymak akıllıca olacaktır.
Bir sonraki sayımızda görüşmek üzere, kendinize iyi bakın.